Question

ABCD is a square of side $2m$. Charges of $5nC$, $10nC$ and $- 5nC$ are at corners A, B and C respectively. What is the work done in transferring a charge of $5\mu C$ from D to the point of intersection of the diagonals?

Answer 1

Here, the system consists of four charges out of which the position of one charge is being changed. As the particles are charged, they possess an electrostatic energy among themselves. This energy is the electrostatic potential energy. This energy depends on the relative positions of the charges. So, if you want to change the position of any charge, you need to work against this electrostatic potential energy.

Complete step by step answer:

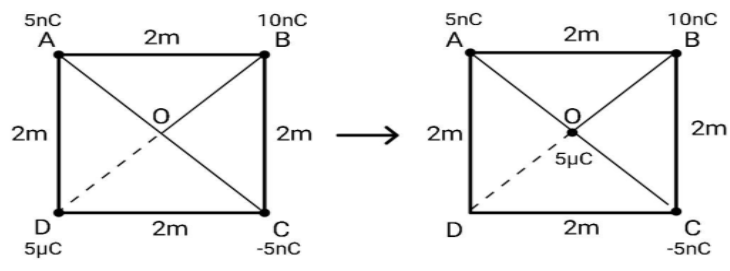
Potential energy is an energy of a system, against which a work is done in order to bring changes. Hence, we say that the work required will be equal to the change in the potential energy of the system. Mathematically,
$W = \Delta U \\\ \Rightarrow W = {U_f} - {U_i} \\\$
The potential energy can be written in terms of potential. Mathematically,
$U = qV$
Therefore, we can write ${U_f} = q{V_f}$ and ${U_i} = q{V_i}$.
In this case, the only change happening is the position of the charge $5\mu C$ from point D to the centre of the square. Hence, we conclude that the work done will be equal to change in the potential energy related to the charge $5\mu C$.
Let ${q_1}$ be the charge at point A, ${q_2}$ is the charge at point B, ${q_3}$ is the charge at point C.
Now, the potential energy of the $5\mu C$charge at point D is given as
${U_D} = q{V_D} \\\ \Rightarrow {U_D} = q\left( {\dfrac{{{q_1}}}{{4\pi {\varepsilon _o}{r_1}}} + \dfrac{{{q_2}}}{{4\pi {\varepsilon _o}{r_2}}} + \dfrac{{{q_3}}}{{4\pi {\varepsilon _o}{r_3}}}} \right) \\\ \Rightarrow {U_D} = \dfrac{q}{{4\pi {\varepsilon _0}}}\left( {\dfrac{{{q_1}}}{{{r_1}}} + \dfrac{{{q_2}}}{{{r_2}}} + \dfrac{{{q_3}}}{{{r_3}}}} \right) \\\ \Rightarrow {U_D} = 5 \times {10^{ - 6}} \times 9 \times {10^9}\left( {\dfrac{{5 \times {{10}^{ - 9}}}}{2} + \dfrac{{10 \times {{10}^{ - 9}}}}{{2\sqrt 2 }} + \dfrac{{( - 5 \times {{10}^{ - 9}})}}{2}} \right) \\\ \Rightarrow {U_D} = 159.099\mu J \\\$
And the potential energy of the $5\mu C$charge at point O is given as
$\Rightarrow {U_O} = q\left( {\dfrac{{{q_1}}}{{4\pi {\varepsilon _0}{r_1}'}} + \dfrac{{{q_2}}}{{4\pi {\varepsilon _0}{r_2}'}} + \dfrac{{{q_3}}}{{4\pi {\varepsilon _0}{r_3}'}}} \right) \\\ \Rightarrow {U_O} = \dfrac{q}{{4\pi {\varepsilon _0}}}\left( {\dfrac{{{q_1}}}{{{r_1}'}} + \dfrac{{{q_2}}}{{{r_2}'}} + \dfrac{{{q_3}}}{{{r_3}'}}} \right) \\\ \Rightarrow {U_O} = 5 \times {10^{ - 6}} \times 9 \times {10^9}\left( {\dfrac{{5 \times {{10}^{ - 9}}}}{{\sqrt 2 }} + \dfrac{{10 \times {{10}^{ - 9}}}}{{\sqrt 2 }} + \dfrac{{( - 5 \times {{10}^{ - 9}})}}{{\sqrt 2 }}} \right) \\\ {U_O} = 318.198\mu J \\\$
Here, ${q_1}$ is the charge at point A, ${q_2}$ is the charge at point B, ${q_3}$ is the charge at point C.
The work done will be $W = {U_f} - {U_i}$. Here ${U_f} = {U_O}$ and ${U_i} = {U_D}$
$\Rightarrow W = 318.198 - 159.099 \\\ \therefore W = 159.099\mu J \\\$
Hence, the work done in transferring a charge of $5\mu C$ from D to the point of intersection of the diagonals is $159.099\mu J$.

Note:
Here, the initial velocity and the final velocity of the charge $5\mu C$ is zero, implying the change in kinetic energy is zero or the initial and final both the kinetic energies are zero. If they were not zero, we still would have applied the same logic for finding work, but instead of finding only the work required to change the potential energy we would be finding work required to change the potential energy plus the work required to change the kinetic energy.