Solveeit Logo
Login

Question

Question: ABCD is a square of side \[2m\]. Charges of \[5nC, + 10nC\] and \[ - 5nC\] are placed at corners A, ...

ABCD is a square of side 2m2m. Charges of 5nC,+10nC5nC, + 10nC and −5nC - 5nC are placed at corners A, B and C respectively. What is the work done in transferring a charge of 5μC5\mu C from D to the point of intersection of the diagonals.

Explanation

Solution

Here side of the square is given. By using side, firstly we will find the diagonal value. Then we will find the value of potential at point O and D due to all other three charges that are given in this particular question. Then we use the work done formula which is the product of charge and the potential difference (W=v.qW = v.q ).

Complete step by step answer:
Given that, Side of Square ABCD=2m = 2m

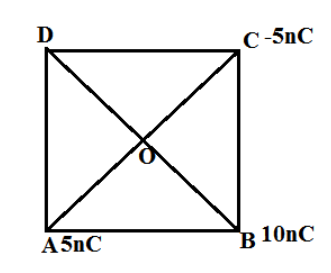
Three charges are given which are placed at the corner of the square (as shown).
Now we can see,
AC=BD=(2)2+(2)2\sqrt {{{(2)}^2} + {{(2)}^2}} =4+4= \sqrt {4 + 4}
=222\sqrt 2 =2.28m = 2.28m
Now, AO=BO=CO=2.8282=1.414m\dfrac{{2.828}}{2} = 1.414m
Potential at O, {V_o} = $$$$\dfrac{1}{{4\pi {\varepsilon _0}}}\left[ {\dfrac{{{q_1}}}{{AO}} + \dfrac{{{q_2}}}{{BO}} + \dfrac{{{q_3}}}{{CO}}} \right]
Potential at D, VD=14πε0[q1AD+q2BD+q3CD]{V_D} = \dfrac{1}{{4\pi {\varepsilon _0}}}\left[ {\dfrac{{{q_1}}}{{AD}} + \dfrac{{{q_2}}}{{BD}} + \dfrac{{{q_3}}}{{CD}}} \right]
Now, we know
Work done=q[vO−vD] = q\left[ {{v_O} - {v_D}} \right]
Charge qq is given and we can find potential at point O and D .
So, W=5×10−6×9×109×[5×10−9[1AO−1AD]+10×10−9[1BO−1BD]] = 5 \times {10^{ - 6}} \times 9 \times {10^9} \times \left[ {5 \times {{10}^{ - 9}}\left[ {\dfrac{1}{{AO}} - \dfrac{1}{{AD}}} \right] + 10 \times {{10}^{ - 9}}\left[ {\dfrac{1}{{BO}} - \dfrac{1}{{BD}}} \right]} \right]
⇒W=45×10−6×109×10−9[5×(11.414−12)+10×(11.414−12.828)]\Rightarrow W = 45 \times {10^{ - 6}} \times {10^9} \times {10^{ - 9}}\left[ {5 \times \left( {\dfrac{1}{{1.414}} - \dfrac{1}{2}} \right) + 10 \times \left( {\dfrac{1}{{1.414}} - \dfrac{1}{{2.828}}} \right)} \right]
⇒W=450×10−6×(11.414−12.828)\Rightarrow W = 450 \times {10^{ - 6}} \times \left( {\dfrac{1}{{1.414}} - \dfrac{1}{{2.828}}} \right)
⇒W=450×10−61.414(1−12)=159.12×10−6Joules\Rightarrow W = \dfrac{{450 \times {{10}^{ - 6}}}}{{1.414}}\left( {1 - \dfrac{1}{2}} \right) = 159.12 \times {10^{ - 6}}Joules
So, 159.12×10−6joules159.12 \times {10^{ - 6}}joules work is done transferring a charge of 5μC5\mu C from D to the point of intersection of diagonals.

Note: Potential difference between two points is the total amount of work is done to transfer a unit charge from one point to another. v=wqv = \dfrac{w}{q}
Here,vv is the potential ,ww is the work done and q is the charge. After knowing the value of potential and charge, we can easily find how much work is done. Work done is calculated in joulesjoules . When 1coulomb1 coulomb of charge is transferred and potential difference is 1volt1volt then the work done is said to be 1joule.1joule.