Question

ABCD is a square of side 0.2m. Point charges $+2\times {{10}^{\circ }}C,+4\times {{10}^{\circ }}C$ and $8\times 10''C$ are located at the corners A, B and C respectively of the square. What is the work done in transferring a charge of $2\times {{10}^{0}}C$ from D to the point of intersection of the diagonals of the square?

Answer 1

First calculate the potentials at the point of intersection of the diagonals of the square and at the point D. The potential at the middle of the square is adequate to the algebraic sum of potentials at the middle due each of the fees individually. Then the work done in transferring the charge is the product of change in potential and magnitude of that transferring charge.
Formula used:
Potential at a point $V=\dfrac{1}{4\pi {{\in }_{0}}}\left[ \dfrac{{{q}_{1}}}{{{d}_{1}}}+\dfrac{{{q}_{2}}}{{{d}_{2}}}+...... \right]$
where,
V is the potential
${{\in }_{0}}$ is the permittivity of free space
${{q}_{1}},{{q}_{2}},{{q}_{3}},....$ are the magnitude of charges .
${{d}_{1}},{{d}_{2}},{{d}_{3}},........$ re the distance between the charges.
Work done, $W=q\left[ {{V}_{2}}-{{V}_{_{1}}} \right]$
${{V}_{2}}-{{V}_{1}}$ is the potential difference.

Complete answer:

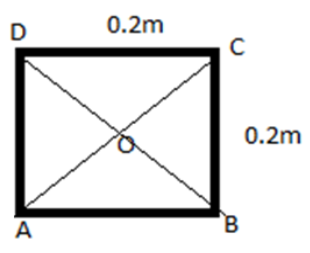
In the figure above AC and BD are the diagonals of the square. Therefore,
AC=BD
$\Rightarrow$ $\sqrt{{{0.2}^{2}}+{{0.2}^{2}}}=\sqrt{0.08}=0.28m$
Then AO,CO and BO are the half length of the diagonal AC and BD respectively.
Then,
AO = BO =CO
$\Rightarrow$ $\dfrac{0.28}{2}=0.14m$
Potential at O , ${{V}_{o}}=\dfrac{1}{4\pi {{\in }_{0}}}\left[ \dfrac{{{q}_{1}}}{AO}+\dfrac{{{q}_{2}}}{BO}+\dfrac{{{q}_{3}}}{CO} \right]$
$=9\times {{10}^{9}}\left[ \dfrac{2\times {{10}^{0}}}{0.14}+\dfrac{4}{0.14}+\dfrac{8\times {{10}^{11}}}{0.14} \right]$
$=5.143\times {{10}^{22}}volts$
Thus,
Potential at D, ${{V}_{D}}=\dfrac{1}{4\pi {{\in }_{0}}}\left[ \dfrac{{{q}_{1}}}{AD}+\dfrac{{{q}_{2}}}{BD}+\dfrac{{{q}_{_{3}}}}{CD} \right]$
$=9\times {{10}^{9}}\left[ \dfrac{2}{0.2}+\dfrac{4}{0.2}+\dfrac{8\times {{10}^{11}}}{0.2} \right]$
$=3.6\times {{10}^{22}}volts$
Work done, $W=q\left[ {{V}_{0}}-{{V}_{D}} \right]$
$=2\left[ 5.143\times {{10}^{22}}-3.6\times {{10}^{22}} \right]$
$\Rightarrow W=3.086\times {{10}^{22}}Joules$

Hence, the work done in transferring the charge is $3.086\times {{10}^{22}}Joules$ .

Note:
Potential at a point is not due to a single charge. It is the algebraic sum of potentials at the center due each of the charges individually. The work done is calculated in Joules and potential difference is in volts.