Question
Question: ABCD is a square of side 0.2m. Charges of \(2\times {{10}^{-9}}\), \(4\times {{10}^{-9}}\) and \(8\t...
ABCD is a square of side 0.2m. Charges of 2×10−9, 4×10−9 and 8×10−9 coulomb are placed at the corners A, B and C respectively. Calculate the work required to transfer a charge of 2×10−9 coulomb from corner D to the centre of the square.
Solution
You could use the superposition principle to find the potential at corner D and centre O due to the system of charges. Also, you could find the potential difference between the two points by simply subtracting the two potentials from each other. From the definition of potential difference we get the work done as the product of charge and potential difference. Now, you substitute and get the answer.
Formula used:
Potential due to a system of charges (superposition principle),
V=4πε01(r1q1+r2q2+r3q3+...+rnqn)
Expression for potential difference,
ΔV=qW
Complete answer:
We are given a square of side 0.2 m with charges kept in each of its corners.
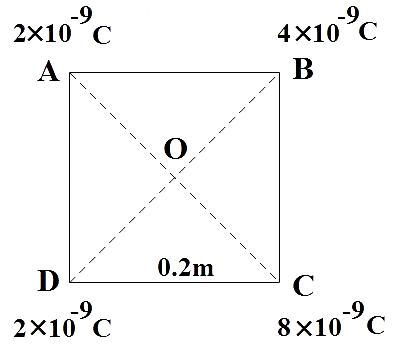
From the diagram, using Pythagorean theorem we get the diagonals of the given square AC and BD as,
AC=BD=(0.2)2+(0.2)2
AC=BD=0.08=0.28m
With our prior knowledge in geometry we know that diagonals of a square bisect each other. Therefore,
DO=BO=AO=CO=20.28=0.14m
We know that potential at given point due to charge Q is given by,
V(r)=4πε01rQ …………….. (1)
When it comes to a system of charges (q1,q2,q3,...,qn) with position vectors(r1,r2,r3,...,rn)with respect to some point, we have to apply superposition principle. As per the superposition principle, the potential due to a system of charges is the sum of the potentials due to individual charges. Let:
Potential due toq1 ,
V1=4πε01r1q1
Potential due toq2 ,
V2=4πε01r2q2
Potential due toqn,
Vn=4πε01rnqn
Then, by superposition principle,
V=V1+V2+V3+...+Vn
V=4πε01(r1q1+r2q2+r3q3+...+rnqn) …………………. (2)
In the given question we have a system consisting of 4 charges. As a first step let us find potential due charges at A, B, and C on point D.
Potential at D due toqA ,
VA=4πε01ADqA ………………. (3)
Potential at D due toqB ,
VB=4πε01BDqB ………………… (4)
Potential at D due toqC ,
VC=4πε01CDqC ……………………. (5)
Adding (3), (4) and (5), we get the total potential at D as,
VD=4πε01(ADqA+BDqB+CDqC) ………………… (6)
Similarly, we get total potential at centre O as,
VO=4πε01(AOqA+BOqB+COqC) ………………………. (7)
From the definition of potential difference between two points we know that it is the work done in order to bring a charge q from one point to the other point. It can be expressed as,
ΔV=qW ………………. (8)
In the given question we are asked to find work done W to bring charge ‘qD’ from D to O. Equation (8) now becomes,
W=qD×ΔV=qD(V0−VD) ……………… (9)
Subtracting (6) from (7), we get,
VO−VD=4πε01(qA(AO1−AD1)+qB(BO1−BD1)+qC(CO1−CD1)) …………………… (10)
Substituting the given values in (10) we get,
VO−VD=4πε01(2×10−9(0.141−0.21)+4×10−9(0.141−0.281)+8×10−9(0.141−0.21))
VO−VD=4πε01(10×10−9(0.21)+4×10−9(3.57))
VO−VD=9×109×16.38×10−9=147.42V ………………………… (11)
Substituting qD=2×10−9C and equation (11) in (9), we get,
W=2×10−9×147.96=294.84×10−9J
Hence, we get the work required to transfer a charge of 2×10−9 coulomb from corner D to the centre of the square as 294.84×10−9J .
Note:
Since all the given quantities are in their SI units, we get the solution also in its SI units, that is, we get the work done in joules. Though, not all the required distances are given, one could use their prior knowledge in geometry to find them. The calculations may appear messy but the concept behind the solution is really simple, we are only using the superposition principle and the definition of potential difference to solve this problem.
