Question
Question: ABCD is a rhombus such that \[\angle \text{ACB}={{40}^{\circ }}\ then \\\angle \text{ADB}\] is ? !...
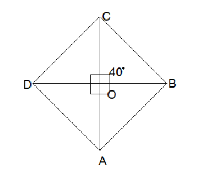
ABCD is a rhombus such that ∠ACB=40∘ then∠ADB is ?
A. 40∘
B. 50∘
C. 45∘
D. None of these
Solution
To find the value of ∠ADB, we first find the value of ∠CBD by using the formula of sum of all the angles equal to 180∘ and after finding the value of angle ∠CBD, we use the alternative angle method where we find the value of ∠ADB.
Complete step by step solution:
Let us draw the diagram and according to the diagram given, we will find the value of the angle ∠CBD. To find the ∠CBD, we first check the triangle CBOwhich contains the angle ∠OCB and ∠COB i.e. 40∘ and 90∘ respectively.
Hence, the value of the angle ∠CBD, we use the formula of the sum of the angle equal to 180∘ where we put the values in the formula as:
⇒∠C+∠O+∠B=180∘
⇒40∘+90∘+∠B=180∘
⇒∠B=180∘−130∘
⇒∠B=50∘
Now that we have the value of ∠B, we can find the value of the ∠D by using the alternate angle method where the angle CBD and BDA are the same. Therefore, the value angle BDA is also given as 50∘.
Note: Rhombus like square have equal sides but the outer angles are not same hence, the outer angle of a rhombus can’t be deemed as 90∘ and similarly student may go wrong if they try to take the outer angles as 90∘ and start their questions with it.
