Question

ABCD is a quadrilateral.E is the point of intersection of the line joining the middle points of the opposite sides. If O is any point then $O\bar A + O\bar B + O\bar C + O\bar D$ =
A. 4$O\bar E$
B. 3$O\bar E$
C. 2$O\bar E$
D. $O\bar E$

Answer 1

Hint- In this question, first we will make the diagram. After this, we will use the results of geometry that the line joining the middle points of the opposite face of the quadrilateral will be the mid point of the line and also the mid point of the diagonals to write the relation between different parts.

Complete step-by-step answer:
The diagram of question is given below:

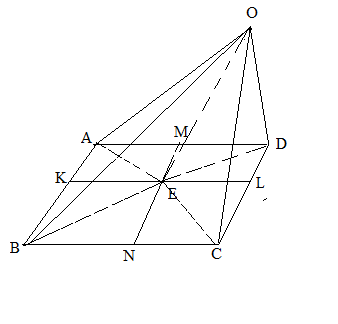
It is given that:
ABCD is a quadrilateral and KL is the line joining the midpoint of the opposite face AB and CD. Similarly, MN is the line joining the midpoint of AD and BC.
E is the point of intersection of line MN and KL.
It is given a point O outside.
We have constructed the line OA,OB,OC,OD and OE.
In a quadrilateral, we know that:
The point of intersection of lines joining the mid point of opposite faces of the quadrilateral will be the mid point of the corresponding lines and also the midpoint of the diagonals.
Therefore we can write:
$E\vec L = - E\vec K$ and $E\vec M = - E\vec N$ ($\because$ they are equal and opposite) (1)
Also,
$E\vec A = - E\vec C$ and $E\vec B = - E\vec D$ ($\because$ they are equal and opposite) (2)
In $\vartriangle$OEA
$O\vec E + E\vec A = O\vec A$ (3)
In $\vartriangle$OEB
$O\vec E + E\vec B = O\vec B$ (4)
In $\vartriangle$OEC
$O\vec E + E\vec C = O\vec C$ (5)
In $\vartriangle$OED
$O\vec E + E\vec D = O\vec D$ (6)
Adding the equation 1,2 3 and 4, we get:
$E\vec A + E\vec B + E\vec C + E\vec D + 4O\vec E = O\vec A + O\vec B + O\vec C + O\vec D$ (7)
But from equation 2, we can say that:
$E\vec A + E\vec B + E\vec C + E\vec D$ =0
Therefore, from equation 7 we can write:
$O\vec A + O\vec B + O\vec C + O\vec D = 4O\vec E$
So, option A is the correct answer.

Note- In this question, first you must make the diagram so that the things get clear. You must note down that we are dealing here vectorially and thus have taken negative signs for writing equations 1 and 2. You should know that E is also the mid point of the diagonals AC and BD.