Question

ABCD is a parallelogram. L is a point on BC which divides BC in the ratio 1:2. AL intersects BD at P. M is a point on DC which divides DC in the ratio 1:2 and AM intersects BD in Q. $Point P divides AL in the ratio$
A.1:2$$$$$ B.1:3 C.$3:1
D.$2:1$$$$$

Answer 1

We use property of ratio to have$BL:BC=1:3$. We prove the similarity of triangles APB and LPD using equality of alternate angles and vertically opposite angles. We use proportionality of length of sides $\dfrac{AP}{LP}=\dfrac{AD}{BL}$ and the use equality of sides in a parallelogram to find $AP: LP$.$$$$

Complete step-by-step solution:
We draw the diagram of the required parallelogram ABCD .$$$$

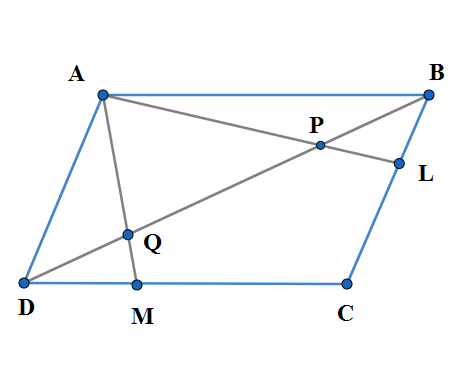
We are given the question that. L is the point on BC which divides BC in the ratio 1:2. So we have
$BL:CL=2:1$
We know from the property of ratio that $a:b=ak:bk$ for any non-zero integer $k$. So let us have $BL=2k,CL=k$ then we have $BC=BL+CL=2k+k=3k$. Now we have;
$\dfrac{BL}{BC}=\dfrac{k}{3k}=\dfrac{1}{3}....\left( 1 \right)$
Let us observe the triangles APB and LPD. We have the vertically opposite angles subtended at the point P which are always equal. So we have;
$\angle APB=\angle LPD$
We know that opposite sides of a parallelogram are equal. So we have parallel sides AD and BC and the transversal AL which makes alternate angles $\angle PDA,\angle PBL$. Since alternate angles are always equal, we have ;
$\angle PDA=\angle PBL$
So by angle-angle or AA criterion we have;
$\Delta APD\sim \Delta LPB$
Since in similar triangles the opposite sides will be in equal ratio, we have opposite sides of the equal angles $\angle PDA=\angle PBL$ and $\angle APB=\angle LPD$ in proportion as;
$\dfrac{AP}{LP}=\dfrac{AD}{BL}$
Since opposite sides of a parallelogram are equal we have $AD=BC$. Now we replace AD by BC in the above step to have;

& \Rightarrow \dfrac{AP}{LP}=\dfrac{BC}{BL} \\\ & \Rightarrow \dfrac{AP}{LP}=\dfrac{1}{\dfrac{BL}{BC}} \\\ \end{aligned}$$ We put the obtained value of $\dfrac{BL}{BC}$ in the above step to have; $$\begin{aligned} & \Rightarrow \dfrac{AP}{LP}=\dfrac{1}{\dfrac{1}{3}} \\\ & \Rightarrow \dfrac{AP}{LP}=\dfrac{3}{1}=3:1 \\\ \end{aligned}$$ **So P divides AL in ratio 3:1 and hence the correct option is C.** **Note:** We must be careful that when we say a point P divides AB in a ratio $a:b$ then it means $AP:PB=a:b$ not $P:B=a:b$. So we should not calculate $A:P: LP=1: 3$. We can similarly prove that Q divides AM in the ratio 3:1. We can solve alternatively if we know about vectors and represent AL and AM as resultant vectors of the sides.