Question

ABCD is a parallelogram in which the coordinates of $A,B$ and $C$ are $\left( 1,2 \right)$ , $\left( 7,-1 \right)$ and $\left( -1,-2 \right)$ respectively.
Calculate the area of the parallelogram.

Answer 1

Here, to calculate the area of parallelogram, firstly we will divide this parallelogram into two triangles by drawing a diagonal line and will find the area of triangle by using the formula that is $\frac{1}{2}\left| {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right|$ . Since, the diagonal divides parallelograms into two equal triangles. So, the area of the triangle is double the area of the triangle.

Complete step-by-step answer:
Since, we need to find the area of the parallelogram, we draw a diagonal line from point $A$ to point $C$ . It will divide the parallelogram into two equal triangles that are $\Delta ABC$ and $\Delta ADC$ . Since, $area\left( \Delta ABC \right)=area\left( \Delta ADC \right)$ . So, we will use the formula to get the area of $\Delta ABC$ as:
$\Rightarrow area\left( \Delta ABC \right)=\dfrac{1}{2}\left| {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right|$

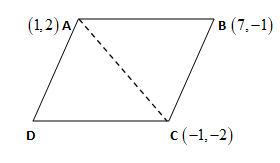
Here, we will use the coordinates of $A,B$ and $C$ as $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ and $\left( {{x}_{3}},{{y}_{3}} \right)$ respectively.
$\Rightarrow area\left( \Delta ABC \right)=\dfrac{1}{2}\left| 1\left( -1-\left( -2 \right) \right)+7\left( -2-2 \right)+\left( -1 \right)\left( 2-\left( -1 \right) \right) \right|$
Now, we will do required calculation as:
$\Rightarrow area\left( \Delta ABC \right)=\dfrac{1}{2}\left| 1\left( -1+2 \right)+7\left( -2-2 \right)-1\left( 2+1 \right) \right|$
Now, we will do the calculation for small brackets as:
$\Rightarrow area\left( \Delta ABC \right)=\dfrac{1}{2}\left| 1\left( 1 \right)+7\left( -4 \right)-1\left( 3 \right) \right|$
Here, we will open the bracket as:
$\Rightarrow area\left( \Delta ABC \right)=\dfrac{1}{2}\left| 1-28-3 \right|$
Now, we will precede the calculation as:
$\Rightarrow area\left( \Delta ABC \right)=\dfrac{1}{2}\left| 1-31 \right|$
$\Rightarrow area\left( \Delta ABC \right)=\dfrac{1}{2}\left| -30 \right|$
Here, we will remove mod and the value of mod is always positive as:
$\Rightarrow area\left( \Delta ABC \right)=\dfrac{1}{2}\times 30$
Now, we will have the area of triangle from the above step as:
$\Rightarrow area\left( \Delta ABC \right)=15$
As we know that the diagonal of the parallelogram divides the parallelogram into two equal triangles. So, the area of the Parallelogram is double the area of any one triangle as:
$\Rightarrow \text{Area of parallelogram }=2\times area\left( \Delta ABC \right)$
Now, we will use the area of triangle in the above formula as:
$\Rightarrow \text{Area of parallelogram }=2\times 15$
Here, we will complete the calculation as:
$\Rightarrow \text{Area of parallelogram }=30$
Hence, the area of parallelogram is $30$ square unit.

Note: Since, we does not have the coordinates of point $D$ , otherwise we can use the formula from the diagram as the area of parallelogram is equal to the sum of the area of both triangles as:
$\Rightarrow area\text{ }of\text{ }\square ABCD=area\left( \Delta ABC \right)+area\left( \Delta ADC \right)$

Or, we can use the formula of the area of parallelogram as:
$\Rightarrow area\text{ }of\text{ }\square ABCD=base\times height$