Question

ABCD is a parallelogram. In which side AB is produced to E so that BE = AB. Prove that ED bisects BC.

Answer 1

Hint: To solve the question, we have to apply the properties of parallelogram to the given parallelogram ABCD to understand that AB, CD are the parallel sides and BC, AD are parallel to each other. Thus, we can apply basic proportionality theorem, SAS symmetry, using this information to arrive at the answer to the given question.

Complete step-by-step answer:
We know that a parallelogram has a pair of equal-parallel sides.
Thus, AB is parallel and equal to CD and BC is parallel and equal to side AD.
AB = CD, BC = AD
Let ED interest the side BC at point F.

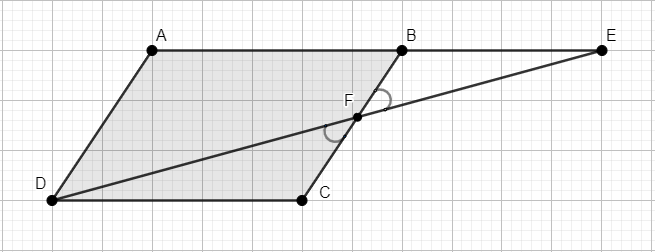
Consider the triangle AED,
Given that B is middle point of AE which implies AB = BE
Thus, BE = CD since AB = CD
BF is parallel to AD since BC is parallel to AD.
We know that, the basic proportionality theorem states that if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio.
By applying this theorem to the triangle AED, we get
$\dfrac{AB}{BE}=\dfrac{DF}{FE}$
Thus, DF = FE
We know that for a pair of intersecting lines vertically opposite angles are equal.
Thus, we get
$\angle BFE=\angle DFC$
We know that by SAS (Side-Angle-Side) symmetry which states two triangles are congruent if two corresponding sides and one corresponding angle are equal.
Thus, we get $\Delta BEF,\Delta DFC$ are congruent
Since DF = FE, BE = CD and $\angle BFE=\angle DFC$
We know that for congruent triangles corresponding sides are equal.
Thus, we get BF = FC = half of BC
Thus, F bisects the side BC.
Hence, ED bisects BC.

Note: The possibility of mistake can be not analysing the given information of the parallelogram and apply the properties of parallelogram. The other possibility of mistake can be not applying the basic proportionality theorem, SAS symmetry which eases the procedure of solving.