Question

ABCD is a parallelogram. If the coordinates of A, B, C are (-2,-1), (3,0) and (1,-2) respectively. Find coordinates of D.

& \text{A}.\text{ }\left( +\text{4},+\text{3} \right) \\\ & \text{B}.\text{ }\left( -\text{4},+\text{3} \right) \\\ & \text{C}.\text{ }\left( +\text{4},-\text{3} \right) \\\ & \text{D}.\text{ }\left( -\text{4},-\text{3} \right) \\\ \end{aligned}$$

Answer 1

Here, we are given a parallelogram ABCD. Three of the coordinates of the vertices are given and we have to find coordinates of the fourth vertex. We will use the theorem that, diagonals of a parallelogram bisects each other. For using this, we will use the midpoint formula to equate mid-points of both diagonal. Midpoint formula is given by:
If $\left( {{x}_{1}},{{y}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right)$ are two given coordinates and we have to find midpoint of the line joining them, it will be given by $\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$.

Complete step-by-step answer:
We are given three coordinates of parallelogram ABCD which are A (-2,-1), B (3,0) and C (1,-2). We have to find coordinates of D.

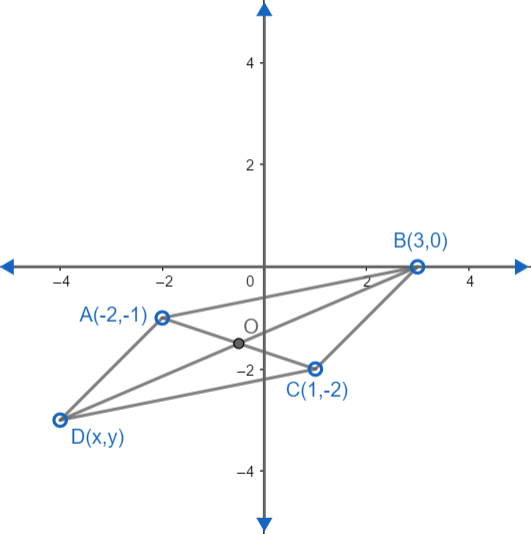
As we know, diagonals of a parallelogram bisect each other. Therefore, midpoint of AC will be equal to midpoint of BD.
As we have to find coordinates of D, let them be as (x, y).
Therefore, midpoint of AC = midpoint of BD.
Using midpoint formula we get:

& \left( \dfrac{-2+1}{2},\dfrac{-1-2}{2} \right)=\left( \dfrac{3+x}{2},\dfrac{0+y}{2} \right) \\\ & \Rightarrow \left( \dfrac{-1}{2},\dfrac{-3}{2} \right)=\left( \dfrac{3+x}{2},\dfrac{y}{2} \right) \\\ \end{aligned}$$ Comparing above terms we conclude that, $$\left( \dfrac{-1}{2}=\dfrac{3+x}{2} \right)\left( \dfrac{-3}{2}=\dfrac{y}{2} \right)$$ Solving both, we get: $$\dfrac{-1}{2}=\dfrac{3+x}{2}$$ Multiplying both sides by 2 we get: $$\begin{aligned} & -1=3+x \\\ & \Rightarrow x=-1-3 \\\ & \Rightarrow x=-4 \\\ \end{aligned}$$ Now, $$\dfrac{-3}{2}=\dfrac{y}{2}$$ Multiplying both sides by 2, we get: $$\begin{aligned} & -3=y \\\ & \Rightarrow y=-3 \\\ \end{aligned}$$ Therefore, $\left( x,y \right)=\left( -4,-3 \right)$ So, coordinates of D are (-4,-3). Hence, D is the correct answer. **So, the correct answer is “Option D”.** **Note:** Students should carefully apply the midpoint formula as there are chances of making plus minus mistakes here. Also, students should learn all properties of parallelogram and other quadrilaterals also. Students should always draw figures for better understanding.