Question

ABC is an equilateral triangle of side 6 cm. If a circle of radius 1 cm is moving inside and along the sides of the triangle, then the locus of the centre of the circle is an equilateral triangle of side_______.
A) 5 cm
B) 4 cm
C) $\left( 6-2\sqrt{3} \right)cm$
D) $\left( 3+\sqrt{3} \right)cm$

Answer 1

Hint: As the circle moves inside the triangle along with sides the centre of that circle also makes the shape of the triangle. So, we need to find the side length of that triangle as the circle moves in the shape of the equilateral triangle and the centre also moves in the same shape. The side length of the equilateral triangle will be the same. So, by using the concept of radius and side lengths of the main triangle, apply some trigonometry as angle is known to you. The side angles for an equilateral triangle will be 60 degrees. Drop perpendicular from centre on to original triangle.
Complete step-by-step answer:
Locus: In geometry locus is a set of points, whose location satisfies or is determined by one or more specified conditions. In other words, the set of points satisfying some particular property is called Locus.

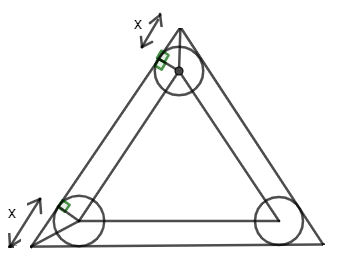
Here the property is centred on a triangle which is inside a triangle. Drop perpendicular from the centre you mark distance as x.
As outside triangle length $=6cm$
Inside triangle length $=6-2x$
As you can see, radius bisects the angle into two angles of 30 degrees.
As we can see the original side is tangent to the circle the line perpendicular will be normal.
Normal passes through the centre. So, that perpendicular length will be equal to radius.
Given radius is 1 cm. So, applying $\tan$ to that 30 degrees, we get:
$\tan 30=\dfrac{1}{x}=\dfrac{1}{\sqrt{3}}$
From this, we get the value of x as $\sqrt{3}cm$.
So, side length of original triangle is $6-2x$
By substituting the value of x in above condition
Side length $=6-2\sqrt{3}\text{ cm}$
So, the side length of the triangle is $\left( 6-2\sqrt{3} \right)\text{ cm}$.
Therefore, option (C) is correct.
Note: Here the student must have an idea of getting a perpendicular line that is normal and as it passes through the centre and its length is equal to the radius of the moving circle (given 1cm).
Don’t forget to take the x at both sides of the triangle as the circle touches all sides.