Question

ABC is a triangular park with AB =AC = 100 meters. A vertical tower is situated at mid-point of BC. If the angle of elevation of the top of the top of the tower at A and B are ${{\cot }^{-1}}\left( 3\sqrt{2} \right)$ and ${{\operatorname{cosec}}^{-1}}\left( 2\sqrt{2} \right)$ respectively, then the height of the tower in meters is.
(a) $10\sqrt{5}$
(b)$\dfrac{100}{3\sqrt{3}}$
(c) 20
(d) 25

Answer 1

To solve this question, first we will make the diagram and label it properly according to the data given in the question.. After that we will evaluate the length of AP = x and length BP in terms of h by using values ${{\cot }^{-1}}\left( 3\sqrt{2} \right)$ and ${{\operatorname{cosec}}^{-1}}\left( 2\sqrt{2} \right)$ as we know that if we have triangle right angled at vertex B, then $\cot A=\dfrac{Base}{Perpendicular}$ and $\operatorname{cosec}A=\dfrac{Hypotenuse}{Perpendicular}$ . Then in the triangle, QBP will use Pythagoras theorem to evaluate length PB. After that we will apply Pythagoras theorem in triangle APB, to get the value of h by using values of AB = 100m, PB and AP = x.

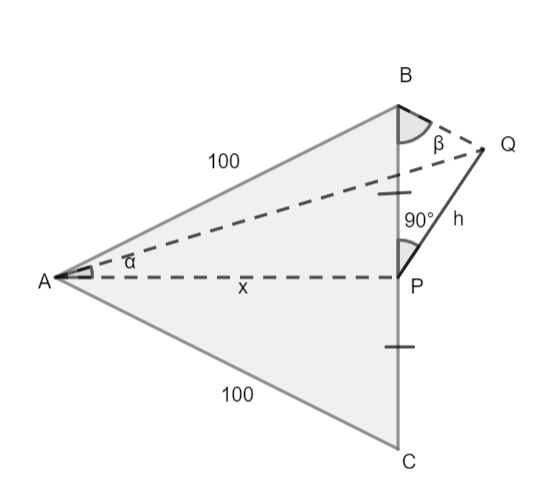
Complete step-by-step answer:
Now, from the figure we can easily see that ABC is a triangular park, with sides AB and AC and BC, where AB = AC = 100m. Let height of tower be PQ = h meters, let vertical distance from foot of tower to vertex of park A be x meter. Also, as the tower is in the middle of side BC so, we can say BP = PC.
Let, the angle of elevation from vertex B to top of tower be $\angle QBP=\beta$ and angle of elevation from vertex A to top of tower be $\angle QAP=\alpha$.
Now, in question it is given that the angle of elevation of the top of tower at A is equals to ${{\cot }^{-1}}\left( 3\sqrt{2} \right)$.
So, we from figure we can see and say that $\angle QAP=\alpha ={{\cot }^{-1}}\left( 3\sqrt{2} \right)$
Or, $\cot \alpha =\left( 3\sqrt{2} \right)$
In triangle QAP,
$\cot \alpha =\dfrac{x}{h}$
Or, $\dfrac{x}{h}=3\sqrt{2}$
Now, in question it is given that angle of elevation of the top of tower at A is equals to ${{\operatorname{cosec}}^{-1}}\left( 2\sqrt{2} \right)$.
We can see in figure and say that $\angle QBP=\beta ={{\operatorname{cosec}}^{-1}}\left( 2\sqrt{2} \right)$
Or, $\cos ec\beta =2\sqrt{2}$
Now, in triangle QBP,
$\operatorname{cosec}\beta =\dfrac{BQ}{h}$
Or, $2\sqrt{2}=\dfrac{BQ}{h}$
So, $BQ=2\sqrt{2}h$
Applying Pythagoras theorem in triangle QBP, we get
$B{{Q}^{2}}=P{{Q}^{2}}+P{{B}^{2}}$ ,
Substituting values of PQ and BQ, we get
${{\left( 2\sqrt{2}h \right)}^{2}}={{h}^{2}}+P{{B}^{2}}$
On simplifying, we get
${{\left( 2\sqrt{2}h \right)}^{2}}-{{h}^{2}}=P{{B}^{2}}$
$\Rightarrow PB=\sqrt{7}h$
Now, in triangle APB we have $AP=3\sqrt{2}h$ , $PB=\sqrt{7}h$
Applying Pythagoras theorem in triangle APB,
$A{{B}^{2}}=P{{B}^{2}}+A{{P}^{2}}$
Putting values of $AP=3\sqrt{2}h$ , $PB=\sqrt{7}h$, we get
$\Rightarrow {{100}^{2}}={{(3\sqrt{3}h)}^{2}}+{{(\sqrt{7}h)}^{2}}~$
$\Rightarrow {{100}^{2}}={{(3\sqrt{3}h)}^{2}}+{{(\sqrt{7}h)}^{2}}~$
$\Rightarrow {{100}^{2}}=25{{h}^{2}}$
$\Rightarrow {{h}^{2}}=\dfrac{1000}{25}~$
$\Rightarrow {{h}^{2}}=400$
$\Rightarrow h = 20m$

So, the correct answer is “Option C”.

Note: To solve such a question, always make a diagram to visualise the question and mark and label the diagram according to the question as it helps in solving the question more easily and quickly. Always remember that In right angled triangle, we can use Pythagoras theorem, which states that $\text{Hypotenus}{{\text{e}}^{2}}=\text{Perpendicula}{{\text{r}}^{2}}+Bas{{e}^{2}}$. Do not consider the negative value of h, as length cannot be negative in measure. Try not to make any calculation errors.