Question

$ABC$ is a triangle in a plane with vertices $A(2,3,5)\,,\,B( - 1,3,2)\;,\,C(\lambda ,5,\mu )$.if the median through A is equally inclined to the coordinate axes, then the value of $({\lambda ^3} + {\mu ^3} + 5)$ is:
$A)\,1130 \\\ B)\,1348 \\\ C)\,1077 \\\ D)\,676 \\\$

Answer 1

At first find the coordinates of M. then find the direction ratios of median AM. Now use the statement that AM is equally inclined to the coordinate axes and write the direction ratios of AM. Equate both the equations and get your answer.

Complete step-by-step answer:

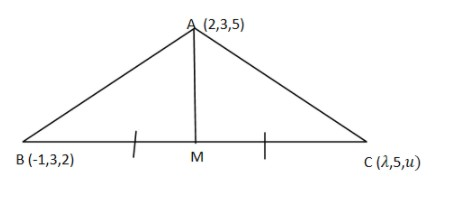
AM is the median of $\Delta ABC$ which means AM bisects BC i.e. M is the midpoint of BC.
So coordinates of M are $\dfrac{{coordinates\,of\,B\, + \,coordinates\,of\,C}}{2}$
$\Rightarrow M \equiv \left( {\dfrac{{\lambda - 1}}{2},\dfrac{{3 + 5}}{2},\dfrac{{\mu + 2}}{2}} \right)$
Hence $\Rightarrow M \equiv \left( {\dfrac{{\lambda - 1}}{2},4,\dfrac{{\mu + 2}}{2}} \right)$
Now we will find direction ratios of AM. Direction ratios of any line AB are
(Coordinates of B - Coordinates of A)
So direction ratios of AM are
$\left( {\dfrac{{\lambda - 1}}{2} - 2,4 - 3,\dfrac{{\mu + 2}}{2} - 5} \right)$
$\left( {\dfrac{{\lambda - 5}}{2},1,\dfrac{{\mu - 8}}{2}} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \to (1)$
As AM is equally inclined to the coordinate axes
Therefore it means direction ratios of $x,y,z$ coordinates are the same.
Let those coordinates be $k$
So direction ratios of AM are $(k,k,k)\,\,\,\,\,\,\,\,\,\, \to (2)$
Now equation (1) and (2) both are direction ratios of AM
Hence they must be equal.
$\Rightarrow \dfrac{{\lambda - 5}}{2} = k\,\,,\,\,k = 1\,\,,\,\,\dfrac{{\mu - 8}}{2} = k$
Using $k = 1\,$ obtained from y-coordinate

$$\Rightarrow \dfrac{{\lambda - 5}}{2} = 1\,\,\,,\,\,\,\dfrac{{\mu - 8}}{2} = 1 \\\ \Rightarrow \lambda - 5 = 2\,\,\,,\,\,\,\mu - 8 = 2 \\\ \Rightarrow \lambda = 7\,\,\,,\,\,\,\mu = 10 \\\$$

Hence value of $({\lambda ^3} + {\mu ^3} + 5)$
$= ({7^3} + {10^3} + 5) \\\ = 1348 \\\$

So, the correct answer is “Option B”.

Note: An important part in the question is this question was to figure out that equally inclination of median AM means their direction ratios are equal. Also you need to know how to calculate the direction ratios.