Question

ABC is a triangle. A circle touches sides AB and AC produced and side BC at X, Y and Z respectively. Show that $AX=\dfrac{1}{2}$ perimeter of $\Delta ABC$.

Answer 1

Hint:Here, first we have to draw the figure. Now, we have to find the perimeter of the $\Delta ABC$ where, Perimeter of $\Delta ABC$ = AB + AC + BC. Next, split AB, AC and BC by looking into the figure. Here, we also have to apply the theorem that the tangents drawn from an external point are equal in length.

Complete step-by-step answer:
Here, we are given that ABC is a triangle and a circle touches sides AB and AC produced and side BC at X, Y and Z respectively.
Now, we have to show that $AX=\dfrac{1}{2}$ Perimeter of $\Delta ABC$.
First let us draw the figure with the given data.

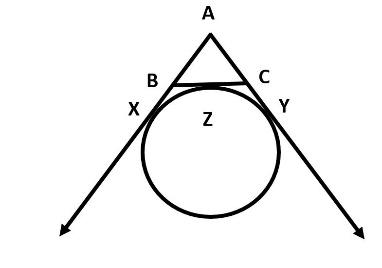
We know that the perimeter of the triangle is the sum of the three sides of the triangle.
Now, for $\Delta ABC$ we have,
Perimeter of $\Delta ABC$ = AB + AC + BC ….. (1)
From the figure AB can be written as:
AB = AX – BX
Similarly, we can write AC and BC as:
AC = AY – CY
BC = BZ + ZC
Substituting all these values in equation (1) we get:
Perimeter of $\Delta ABC$ = (AX – BX) + (AY – CY) + (BZ + ZC)
$\Rightarrow$ Perimeter of $\Delta ABC$ = AX – BX + AY – CY + BZ + ZC …… (2)
We also know that the tangents drawn from an external point are equal in length.
Now, from point B we have the tangents BX and BZ. Hence, we can write:
BX = BZ
Similarly from the point C we have the tangents CZ and CY. So, we can write:
CY = CZ
Now, by substituting all these values in equation (2), we obtain:
Perimeter of $\Delta ABC$ = AX – BZ + AY – CZ + BZ + ZC
Next, by cancellation of BZ and CZ we obtain:
Perimeter of $\Delta ABC$ = AX + AY ……. (3)
From the figure we can say that AX and AY are tangents drawn from an external point A and are equal in length. Therefore, we get:
AX = AY
So, now equation (3) becomes:
Perimeter of $\Delta ABC$ = AX + AX
$\Rightarrow$ Perimeter of $\Delta ABC$ = 2AX
Next, by cross multiplication,
$\Rightarrow \dfrac{1}{2}$ Perimeter of $\Delta ABC$ = AX
That is, AX = $\dfrac{1}{2}$ Perimeter of $\Delta ABC$
Hence, the proof.

Note: Here, at three points the tangents touch the circle. With A as the external point the tangents taken are AX and AY, with B as the external point the tangents taken are BX and BZ and with C as the external point the tangents taken are CZ and CY. The tangents drawn from an external point are equal in length.Hence using this concept we proved the above expression.