Question

ABC is a right angled triangle plane of uniform thickness. The sides are such that $AB > BC$ as shown in the figure. ${I_1},{I_2},{I_3}$ are moments of inertia about $AB$, $BC$ and $AC$, respectively. Then which of the following relations is correct?

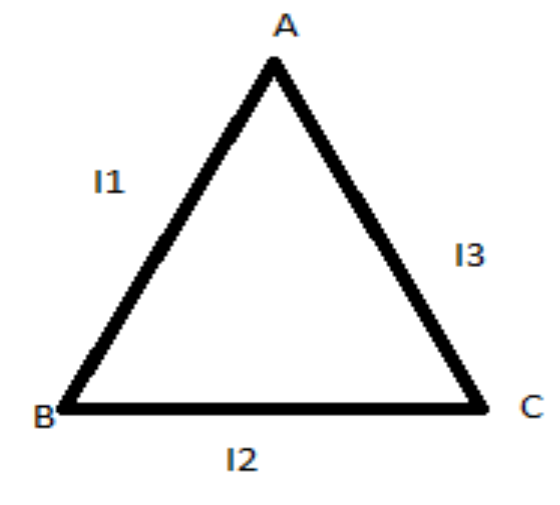
A. ${I_1} = {I_2} = {I_3}$

B. ${I_2} > {I_1} > {I_3}$

C. ${I_3} < {I_2} < {I_1}$

D. ${I_3} > {I_1} > {I_2}$

Answer 1

First let us see what moment of inertia is-
A rigid body’s moment of inertia, otherwise referred to as the mass moment of inertia, angular mass or rotational inertia, is a quantity that specifies the torque necessary for a desired angular acceleration around a rotational axis, analogous to how the mass specifies the force required for a desired acceleration.
The moment of inertia is mathematically given by-
$I = m{k^2}$
where $m =$ mass of the object, $k =$ radius of gyration.

Complete step by step solution:
It is possible to convey a triangle’s moment of inertia in different ways. Typically, there are three phases which can be found. They are-
a. Axis passing through the centroid
b. Axis passing through the base
c. The axis perpendicular to its base
Moment of inertia about any side is $\dfrac{{m{h^2}}} {6}$, where $h$ is the length of the perpendicular from the opposite vertex to the given side/axis.

Given,
ABC is a right angled triangle plane of uniform thickness. The sides are such that $AB > BC$
as shown in the figure. ${I_1},{I_2},{I_3}$ are moments of inertia about $AB$, $BC$ and $AC$, respectively.
Now, let us redraw the triangle as below-

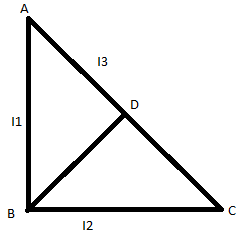
Moment of inertia of a side will be $\dfrac{{m{h^2}}} {6}$
Now if we compare the three heights, we get-
$AB > BC > BD$
So, the order of moment of inertia will be $BC > AB > AC$
Therefore, the answer will be ${I_2} > {I_1} > {I_3}$

Hence, option B is the correct answer.

Note:
In this solution side $AB$ is taken as the axis of rotation for the moment of inertia. If mass distribution from the axis is high, then the moment of inertia will also become greater. Here we have to observe the distance from the axis and their differential masses.