Question

AB is a vertical pole with B at the ground level and A at the top. A man finds that the angle of elevation of the point A from a certain point C on the ground is ${{60}^{\circ }}$. He moves away from the pole along the line BC to a point D such that $CD=7$ m. From D the angle of elevation of the point A is ${{45}^{\circ }}$. Then the height of the pole is
A. $\dfrac{7\sqrt{3}}{2}\left( \sqrt{3}-1 \right)$ m
B. $\dfrac{7\sqrt{3}}{2}\left( \sqrt{3}+1 \right)$ m
C. $\dfrac{7\sqrt{3}}{2\left( \sqrt{3}-1 \right)}$ m
D. $\dfrac{7\sqrt{3}}{2\left( \sqrt{3}+1 \right)}$ m

Answer 1

Hint : We first assume the height of the pillar. We then use trigonometric ratios for the given angles to find the relation between the distances from the pole to the point C and D. We then form the equation and solve that to find the height of the pillar. Use of trigonometric functions strictly depends on the side which we have to find and sides given , depending upon that we use tan , sin and cos.

Complete step-by-step answer :
We first try to draw the scenario for the pillar.

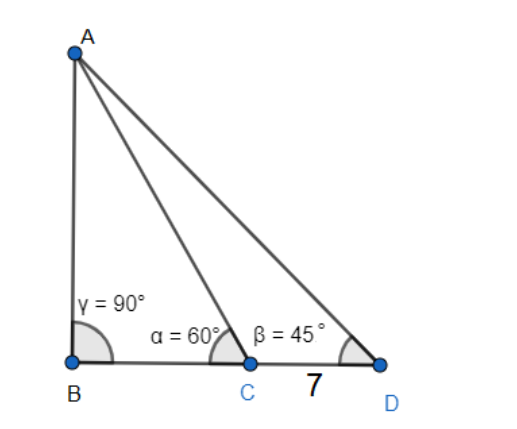
The pillar is AB. We assume the length of the pillar to be $h$.
The distance between the points C and D is 7 m. So, $CD=7$.
At point C and D, the elevation of the top of the pillar is ${{60}^{\circ }}$ and ${{45}^{\circ }}$ respectively. So, $\angle BCA={{60}^{\circ }},\angle BDA={{45}^{\circ }}$.
Now with respect to the angles $\angle BCA={{60}^{\circ }},\angle BDA={{45}^{\circ }}$ and the side of AB, we find the length of the segments BC and BD.
We have
$\begin{aligned} & \dfrac{BC}{AB}=\cot \left( \angle BCA \right)=\cot {{60}^{\circ }} \\\ & \dfrac{BD}{AB}=\cot \left( \angle BDA \right)=\cot {{45}^{\circ }} \\\ \end{aligned}$
We place the values to get
$\begin{aligned} & \dfrac{BC}{h}=\cot {{60}^{\circ }}=\dfrac{1}{\sqrt{3}} \\\ & \dfrac{BD}{h}=\cot {{45}^{\circ }}=1 \\\ \end{aligned}$
On simplification we get $BC=\dfrac{h}{\sqrt{3}},BD=h$.
We know $CD=BD-BC=7$. Putting the values, we get
$\begin{aligned} & h-\dfrac{h}{\sqrt{3}}=7 \\\ & \Rightarrow h\left( 1-\dfrac{1}{\sqrt{3}} \right)=7 \\\ & \Rightarrow h=\dfrac{7\sqrt{3}}{\sqrt{3}-1}=\dfrac{7\sqrt{3}\left( \sqrt{3}+1 \right)}{\left( \sqrt{3}-1 \right)\left( \sqrt{3}+1 \right)}=\dfrac{7\sqrt{3}}{2}\left( \sqrt{3}+1 \right) \\\ \end{aligned}$
The length of the pillars is $\dfrac{7\sqrt{3}}{2}\left( \sqrt{3}+1 \right)$ m.
So, the correct answer is “Option B”.

Note : If a person stands and looks up at an object, the angle of elevation is the angle between the horizontal line of sight and the object. If a person stands and looks down at an object, the angle of depression is the angle between the horizontal line of sight and the object.