Question

AB is a variable line sliding between the coordinate axes in such a way that $A$ lies on the x-axes and $B$ lies on the y-axes. If $P$ is a variable point on $AB$ such that $PA = b$ , $PB = a$ and $AB = a + b$, then determine the equation of the locus of the point $P$.

Answer 1

A locus is the set of all points that satisfy some given condition. When a point is fixed on the variable line, and the line is moved, then the fixed point has the tendency to move in a specific path, that path represents the locus of the given point. It can be any curve or sphere, it depends upon the movement of the variable part. To solve this problem first we will consider arbitrary coordinates of point P as (h,k) then find the relation using given data then replace (h,k) with (x,y) to get the locus.

Complete step by step answer:
We are given that $AB$ is a variable line sliding between the coordinate axes in such a way that $A$lies on the x-axes and $B$ lies on the y-axes. If $P$is a variable point on $AB$such that $PA = b$ , $PB = a$ and $AB = a + b$. Let a line perpendicular from point $P$ to x-axis meet at the point
$N$ and y-axis at the point $M$ .We can represent the given information in the figure shown below:

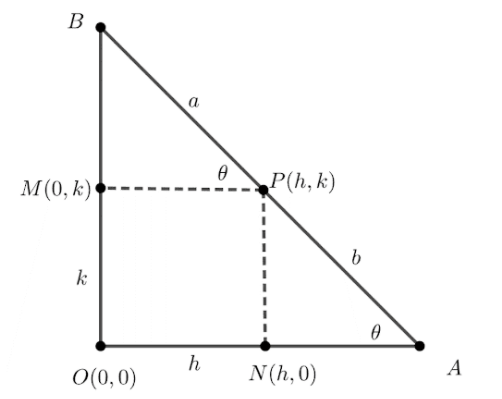
We need to determine the locus of the point $P$.
Let’s consider the arbitrary coordinates of the point $P$ be $(h,k)$, then the coordinates of the point M is $(0,k)$ and the coordinates of the point N is $(h,0)$.
Let the $\angle BPM = \theta$.
Since it is clear that $OA$ lies on the x-axis and segment $MP$ is parallel to the x-axis, hence these two lines are parallel to each other. Line segment $AB$ falls on both the segments $OA$ and $MP$. Then using the property of the corresponding angle, $\angle BPM = \angle PAN = \theta$
In triangle $\Delta PMB$, since it is a right angle triangle,
Using $\sin \theta = \dfrac{{Perpendicular}}{{Hypotenuse}}$ and $\cos \theta = \dfrac{{Base}}{{Hypotenuse}}$
$\sin \theta = \dfrac{{MB}}{{PM}}$ and $\cos \theta = \dfrac{h}{a}$
And in triangle $\Delta PNA$,
$\sin \theta = \dfrac{k}{b}$ and $\cos \theta = \dfrac{{AN}}{b}$
Now from both the triangles we have
$\sin \theta = \dfrac{k}{b}$ and $\cos \theta = \dfrac{h}{a}$
Substitute the above values of $\sin \theta$ and $\cos \theta$ in the trigonometric identity
${\sin ^2}\theta + {\cos ^2}\theta = 1$
${\left( {\dfrac{k}{b}} \right)^2} + {\left( {\dfrac{h}{a}} \right)^2} = 1$
So, the locus of the point $P$is given by
$\dfrac{{{h^2}}}{{{a^2}}} + \dfrac{{{k^2}}}{{{b^2}}} = 1$
Since the coordinates are chosen arbitrarily, so put $h = x,k = y$, hence the locus of the point P comes out to be $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$

Note:
In a right-angled triangle, the values of $\sin \theta = \dfrac{{Perpendicular}}{{Hypotenuse}}$ and $\cos \theta = \dfrac{{Base}}{{Hypotenuse}}$. These trigonometric identities are very useful in solving various questions involving the sides of the triangle. Also they are interrelated to each other.