Question

AB is a potentiometer wire of the length 100cm and the resistance 10ohms. It is connected in the series with the resistance R = 40ohms and a battery of the emf 2V and negligible internal resistance. If a source of the unknown emf E is balanced by the 40cm length of the potentiometer wire, the value of E is:-

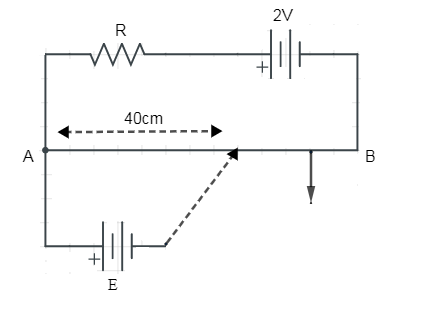
A. 0.8V
B. 1.6V
C. 0.08V
D. 0.16V

Answer 1

In order to solve this question first we have to find the potential gradient then by using potential gradient we will find emf using formula of the potential gradient and emf.

Formula used:

& P.G=\dfrac{V}{L} \\\ & E=P.G.l \\\ & I=\dfrac{V}{R} \\\ & R={{R}_{1}}+{{R}_{2}} \\\ \end{aligned}$$ **Complete step by step solution:** 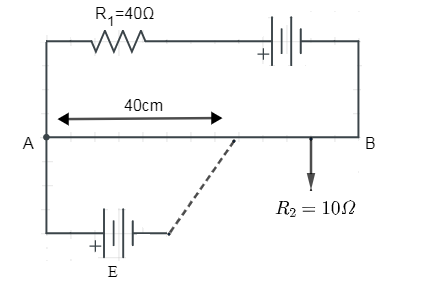 Given data, Length of the potential wire L = 100cm L = 1m (converting cm to m) Resistance of the potentiometer is ${{R}_{2}}=40\Omega $ Battery emf = V = 2V Balance length = l = 40cm $\begin{aligned} & l=\dfrac{40}{100}m\left( \text{converting cm to m} \right) \\\ & l=0.4m \\\ \end{aligned}$ Now formula for the potential gradient is $P.G=\dfrac{V}{L}$ We know that, V = IR Hence, $P.G=\dfrac{IR}{L}...\left( 1 \right)$ Where, P.G. = potential resistance R = resistance in the potentiometer wire. L = length of the potentiometer Now we have to find total current, we know that, $I=\dfrac{V}{{{\operatorname{R}}_{e}}}...\left( 2 \right)$ Here, $\begin{aligned} & {{\operatorname{R}}_{e}}={{R}_{1}}+{{R}_{2}} \\\ & =40+10 \\\ & {{R}_{e}}=50\Omega \\\ & V=2V \\\ \end{aligned}$ Substituting values in the equation (2) we get, $I=\dfrac{2}{50}A$ Now to find the emf at 40cm length we have to use potential gradient formula for the 40cm length $\begin{aligned} & P.G.=\dfrac{E}{l} \\\ & \therefore E=P.G.\times l....\left( 3 \right) \\\ \end{aligned}$ Substitute formula of the equation (1) in the equation (3) $E=\dfrac{I{{R}_{2}}}{L}\times l......\left( 4 \right)$ Now put all the values in the equation (4) $\begin{aligned} & \Rightarrow E=\dfrac{2}{50}\dfrac{\times }{\times }\dfrac{10}{1}\times 0.4 \\\ & \therefore E=0.16V \\\ \end{aligned}$ **Hence, the correct answer is option (D).** **Additional information:** Resistance: When current flows through any conductor, the conductor offers some obstruction to the current and this obstruction is known as electrical resistance and is denoted by R. Resistivity: Electric resistivity is defined as the electrical resistance offered per unit length and unit cross-sectional area at a specific temperature. It is denoted by $\rho $ . **Note:** First we have to convert the length of the potentiometer from cm to m and when we write an equation for 100cm length then we have to put the values of the resistance as the potentiometer resistance don’t mistaken as total or equivalent resistance of the circuit.