Question

AB is a fixed diameter of a circle whose center is O. From C, any point on the circle, a chord CD is drawn perpendicular to AB. Then, as C moves over a semicircle, the bisector of angle OCD cuts the circle in a point that always.
A. Bisects the arc AB
B. Trisects the arc AB
C. Is as far from AB as D
D. Is equidistant from B and C

Answer 1

We can draw the circle with center O diameter AB and chord CD perpendicular to AB. Then we can draw the angle bisector of angle OCD to intersect the circle. Then we can draw the radius to this point to form a triangle. By applying the properties of isosceles triangles and equality of alternate interior angles we can find the ratio at which the angle bisector cuts the arc AB.

Complete step by step answer:

We can draw the circle with center O and diameter AB.

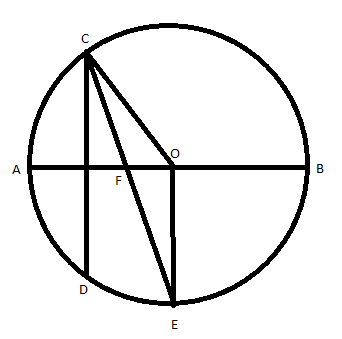
It is given that C is any point on the circle and CD is drawn perpendicular to AB.
We can draw the radius OC to point C. From the figure, CE is the angle bisector of $\angle OCD$, and E is the point it intersects with the circle. We can also draw the radius OE from E.
Now we can consider triangle COE.
We can say the OC=OE as both are the radius of the same circle.
So, the triangle COE is isosceles.
We know that for an isosceles triangle the base angles are equal. So, from this triangle, we get,
$\Rightarrow \angle OEC = \angle OCE$… (1)
It is given that CE is the angle bisector of $\angle OCD$.
$\Rightarrow \angle DCE = \angle OCE$ .. (2)
Equating (1) and (2), we get,
$\Rightarrow \angle DCE = \angle OEC$
From the figure, we can say that CE is a transversal that intersects the line CD and OE.
$\angle DCE$ and $\angle OEC$ are the alternate interior angles.
But we have $\angle DCE = \angle OEC$.
So, CD and OE are parallel lines.
We know that CD is perpendicular to AB. As CD and OE are parallel. So, OE will also be perpendicular to AB.
We know that equal angles subtend equal arcs.
As OE is perpendicular to AB, $\angle AOE = \angle BOE = 90^\circ$ .
As the angles are equal, their arcs will also be equal.
$\Rightarrow arc\,AE = arc\,EB$
Therefore, point E bisects the arc AB.
So, the correct answer is option A.

Note: We must draw a figure and label it for understanding the problem. The distance from the center to any point on the circle will be equal to the radius. The diameter of a circle is the largest chord which passes through the center and equal to twice the radius. We know that the isosceles triangle is a triangle that has 2 sides equal. For an isosceles triangle, the base angles will be equal. Arcs are the parts of a circle. Two equal arcs with the same radius will subtend equal angles at the center and vice-versa.