Question

AB is a double ordinate of parabola $y^2 = 8x$ which passes through the focus S. $\triangle ABC$ is isosceles right angled triangle, where C lies on positive x-axis. Line passing through A and C meets the parabola again at E and line passing through B and C meets the parabola again at D. Then which of the following is/are correct?

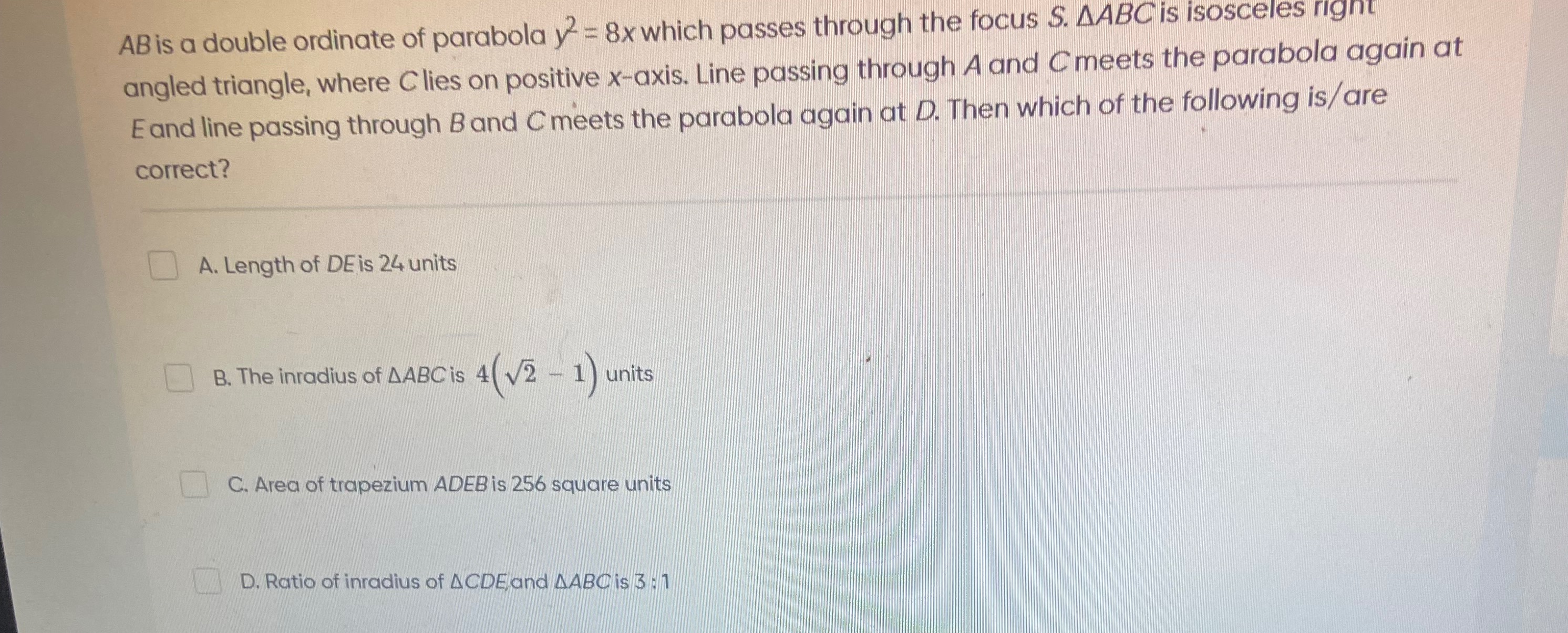
• A. Length of $DE$ is 24 units
• B. The inradius of $\triangle ABC$ is $4(\sqrt{2} - 1)$ units
• C. Area of trapezium $ADEB$ is 256 square units
• D. Ratio of inradius of $\triangle CDE$ and $\triangle ABC$ is 3:1

Answer 1

Answer: (A), (B), (C), (D)

A, B, C, and D

Answer 2

Solution:

1. Parabola and Focus: The parabola is given by

   $$y^2=8x.$$

   Writing it as $y^2 = 4ax$ gives $a=2$ so the focus is $S=(2,0)$.

2. Double Ordinate AB: A double ordinate is a vertical chord. Since this chord passes through the focus, its line is $x=2$. Let the endpoints be

   $$A=(2, y_1) \quad \text{and} \quad B=(2, y_2).$$

   They lie on the parabola so

   $$y_1^2=8\cdot2=16 \quad\text{and}\quad y_2^2=16.$$

   Take $A=(2,-4)$ and $B=(2,4)$.

3. Triangle ABC: The vertex $C$ lies on the positive $x$-axis so $C=(c,0)$, $c>0$. Given that $\triangle ABC$ is an isosceles right triangle, we note:

   $$CA = CB.$$

   With

   $$CA=\sqrt{(c-2)^2+(0+4)^2}=\sqrt{(c-2)^2+16} \quad\text{and}\quad CB=\sqrt{(c-2)^2+(0-4)^2}=\sqrt{(c-2)^2+16},$$

   the triangle is isosceles with right angle at $C$ if

   $$AB^2=CA^2+CB^2.$$

   Here, $AB=8$ so:

   $$64=2[(c-2)^2+16] \quad\Rightarrow\quad (c-2)^2+16=32 \quad\Rightarrow\quad (c-2)^2=16.$$

   Thus, $c-2=4$ (since $c>0$) so $c=6$ and $C=(6,0)$.

4. Finding E on line AC: The line $AC$ through $A=(2,-4)$ and $C=(6,0)$ has slope

   $$m=\frac{0-(-4)}{6-2}=1.$$

   Its equation is

   $$y=x-6.$$

   Substituting $y=x-6$ in the parabola:

   $$(x-6)^2=8x \quad\Rightarrow\quad x^2-12x+36-8x=0 \quad\Rightarrow\quad x^2-20x+36=0.$$

   The solutions are

   $$x=\frac{20\pm\sqrt{400-144}}{2}=\frac{20\pm16}{2}.$$

   Taking $x=2$ (which gives $A$), the other intersection is $x=18$ so

   $$y=18-6=12.$$

   Hence, $E=(18,12)$.

5. Finding D on line BC: The line $BC$ through $B=(2,4)$ and $C=(6,0)$ has slope

   $$m=\frac{0-4}{6-2}=-1.$$

   Its equation is

   $$y=-x+6.$$

   Substituting into the parabola:

   $$(-x+6)^2=8x \quad\Rightarrow\quad x^2-12x+36-8x=0 \quad\Rightarrow\quad x^2-20x+36=0.$$

   Taking the solution $x=2$ gives $B$, the other solution is $x=18$ so

   $$y=-18+6=-12.$$

   Hence, $D=(18,-12)$.

6. Option A (Length of DE): $D=(18,-12)$ and $E=(18,12)$ lie vertically apart. Thus,

   $$DE=|12 - (-12)|=24 \text{ units.}$$

7. Option B (Inradius of $\triangle ABC$): $\triangle ABC$ is right-angled at $C$ with legs $CA=CB$. From point $A$ to $C$:

   $$CA=\sqrt{(6-2)^2+(0-(-4))^2}=\sqrt{4^2+4^2}=4\sqrt2.$$

   In a right triangle the inradius is

   $$r=\frac{a+b-c}{2}.$$

   Here, $a=b=4\sqrt2$ and the hypotenuse $AB=8$. So:

   $$r_{ABC}=\frac{4\sqrt2+4\sqrt2-8}{2}=4(\sqrt2-1).$$

8. Option C (Area of Trapezium $ADEB$): The trapezium $ADEB$ has vertices $A=(2,-4)$, $D=(18,-12)$, $E=(18,12)$, $B=(2,4)$. Notice that sides $AD$ and $BE$ are non‐parallel but the vertical sides $AB$ (from $A$ to $B$) and $DE$ (from $D$ to $E$) are parallel (both vertical).

   • Length of $AB$: $8$ units.
   • Length of $DE$: $24$ units.
   • Horizontal distance between $x=2$ and $x=18$: $16$ units.

   So the area is

   $$\text{Area}=\frac{1}{2}(8+24)\times 16=\frac{1}{2}(32\times16)=256\text{ square units.}$$

9. Option D (Ratio of inradii of $\triangle CDE$ and $\triangle ABC$): In $\triangle CDE$ with vertices $C=(6,0)$, $D=(18,-12)$, and $E=(18,12)$:

   • $CD=\sqrt{(18-6)^2+(-12-0)^2}=\sqrt{144+144}=12\sqrt2.$
   • $CE=\sqrt{(18-6)^2+(12-0)^2}=12\sqrt2.$
   • $DE=24.$

   This is an isosceles right triangle (legs $12\sqrt2$ and hypotenuse $24$). Its inradius is:

   $$r_{CDE}=\frac{12\sqrt2+12\sqrt2-24}{2}=\frac{24\sqrt2-24}{2}=12(\sqrt2-1).$$

   We have $r_{ABC}=4(\sqrt2-1)$. Therefore, the ratio is:

   $$\frac{r_{CDE}}{r_{ABC}}=\frac{12(\sqrt2-1)}{4(\sqrt2-1)}=3.$$

   So, the ratio is $3:1$.

Final Answers:

• A. True
• B. True
• C. True
• D. True

---

Core Explanation: The double ordinate through the focus for $y^2=8x$ gives $x=2$ and points $A=(2,-4)$ and $B=(2,4)$. For $\triangle ABC$ (right angle at $C$ on the positive $x$-axis) using $CA=CB$, we find $C=(6,0)$. The lines $AC$ and $BC$ meet the parabola again at $E=(18,12)$ and $D=(18,-12)$ respectively. Using distance and inradius formulas for right triangles and the trapezium area formula, each option is verified.