Question
Question: AB is 1 meter long uniform wire of \(10\,\Omega \) resistance. The other data shown in the circuit d...
AB is 1 meter long uniform wire of 10Ω resistance. The other data shown in the circuit diagram. Calculate
(a) Potential gradient along AB
(b) Length AO of the wire when the galvanometer shows no deflection.
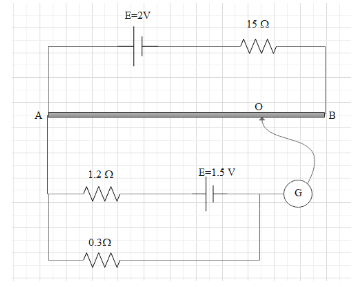
Solution
By using Kirchhoff’s voltage rule we can find the value of current flowing in the circuit. Voltage across AB is the product of current flowing through AB and the resistance of the wire AB. By dividing this voltage with the length, we can find the potential gradient. The potential across length AO of the wire is the same as the potential across the 0.3Ω resistor. Using this we can find the length AO.
Complete answer:
Here we are given a potentiometer circuit. We need to find the potential gradient along AB and the length AO when the galvanometer shows zero deflection.
We know that at the point at which the galvanometer shows zero deflection is the balancing point. Then the total current i from the 2V will be flowing through AB.
Now let us use Kirchhoff’s voltage rule to find the value of this current in this closed circuit.
According to Kirchhoff’s voltage rule the total voltage across a closed circuit will be zero.
Thus, in the closed loop containing wire AB, 15Ω resistor and battery of 2V we have,
2−VAB−VR=0 …………...(1)
Here VAB is the voltage drop across AB and VR is the voltage across 15Ω resistor.
We know that from ohm's law voltage is the product of current and resistance.
So, the voltage across the 15Ω resistance will be
⇒ VR=i×15
Voltage across the wire AB with resistance 10Ω will be
⇒ VAB=i×10
Substituting these values in equation 1 we get
⇒ 2−10i−15i=0
⇒i=0.08A
Thus, the voltage across AB is
⇒ VAB=i×R=0.08×10=0.8V
If you have the potential difference then we can find the potential gradient by dividing the potential with length.
Length of the wire is given as l=1m.
Thus, potential gradient is given as
⇒ Potentialgradient = lVAB
⇒ Potentialgradient = 10.8=0.8V/m
Now we need to find the length of AO which is the balancing length.
Let's consider the total current in the closed circuit involving the resistors 1.2Ω ,0.3Ω and1.5V battery.
Let the current in this circuit be i′ .
If we apply Kirchhoff’s voltage law in this loop, we get
⇒ 1.5−1.2×i′−0.3×i′=0
On solving we get,
⇒ i′=1.51.5=1A
This is the current flowing in this circuit.
Using this we can find the voltage across 0.3Ω resistor as
⇒ V0.3=i′×R
⇒V0.3=1×0.3=0.3V
This voltage across 0.3Ω is the same as the voltage across AO since they are parallel.
Thus,
VAO=0.3V
We know that the voltage across AO is the potential gradient multiplied by length AO. Let this length be denoted as x.
Then we can write
⇒ VAO=Potentialgradient×x
On substituting the values, we get
⇒0.3=0.8×x
∴x=83=0.375m. This is the length of AO when the galvanometer shows zero deflection.
Note:
Here note that while applying Kirchhoff voltage rule, we need to consider closed independent loops. Here we have two independent loops first one is the loop with wire AB resistor 15Ω and battery of 2V. the other loop is that involving the resistors 1.2Ω, 0.3Ω and 1.5V battery. So, we need to apply voltage rules separately in these loops.
