Question
Question: AB and CD are two parallel chords of a circle such that AB = 10 cm and CD = 24 cm. If the chords are...
AB and CD are two parallel chords of a circle such that AB = 10 cm and CD = 24 cm. If the chords are on the opposite sides of the centre and the distance between them is 17 cm, the radius of the circle is:
A. 14cm B. 10cm C. 13cm D. 15cm
Solution
Consider the distance of chord AB from the centre of the circle to be x. The line joining the centre with the midpoint of the chord, the radius of the circle along with the half length segment of the chord will form a right angled triangle. Apply basic trigonometry to obtain the radius of the circle.
Complete step by step answer:
Consider the distance between the centre O and the chord AB as x. Therefore, the distance between centre O and chord CD becomes (17 – x).
The following diagram should be drawn first, as per the information given.
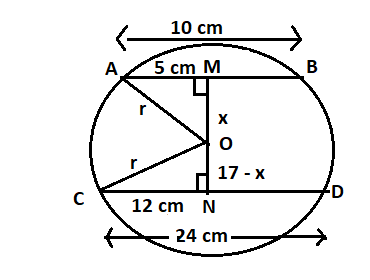
From triangle AMO, using Pythagoras theorem-
AM2+OM2=OA2 52+x2=r2.....(i)
Similarly from triangle OCN
ON2+CN2=ON2 (17−x)2+122=r2.....(ii)
From (i) and (ii)
52+x2=(17−x)2+122 25+x2=289+x2−34x+144 34x=264+144 34x=408 x=12
AS, now we know the value of x, we can use its value in triangle AMO, to obtain r,
52+122=r2 25+144=r2 169=r2 169=r 13=r
The value of r = 13 cm.
So, the correct answer is “Option C”.
Note: The perpendicular line from the centre which meets the chord always intersects the chord at its mid point. This is why we get a right angled triangle. This property of the circle has been used to solve the question.
