Question
Question: AB and CD are two identical rods each of length \( l \) and mass \( m \) joined to form a cross is f...
AB and CD are two identical rods each of length l and mass m joined to form a cross is fixed inside a ring of mass m and radius l/2 . Moment of inertia of the system about a bisector of the angle between the rods (xy) is
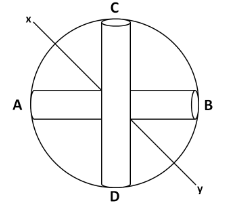
(A) 67ml2
(B) 1213ml2
(C) 12ml2
(D) 245ml2
Solution
To solve this question, we need to find out the moment of inertia of the system about the axis passing through the centre and perpendicular to the plane. We have to use the perpendicular axis theorem for this purpose. Then again using the perpendicular axis theorem and symmetry, we can find out the final value of the moment of inertia about the given axis.
Formula used: The formulae used to solve this question are given by
I=12ml2 , here I is the moment of inertia of a rod of mass m and length l about an axis passing through its centre and perpendicular to its length.
I=MR2 , here I is the moment of inertia of a ring of mass M and radius R about the axis passing through its centre and perpendicular to its plane.
Complete step-by-step solution
Let the moment of inertia be Ixy . Let us define two axes in the given system, namely AB and CD by joining the point A, B and C, D respectively as shown in the below diagram. Also, let us name the point of intersection of these axes as O.
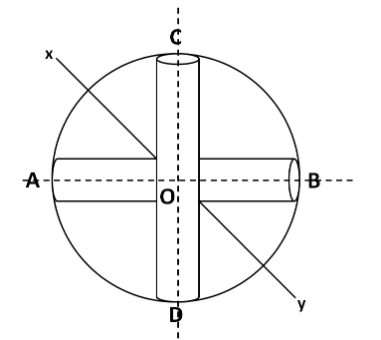
We know that the moment of inertia of a rod about an axis passing through its centre and perpendicular to its length is given by
I=12ml2
So the moment of inertia of the rod CD about the AB axis is given by
IAB=12ml2 ............................(1)
Similarly, the moment of inertia of the rod AB about the CD axis is given by
ICD=12ml2 ............................(2)
Now, let us consider an axis passing through the point O and perpendicular to the plane of the given system, the o-axis. By perpendicular axis theorem, the moment of inertia of the system of the two rods AB and CD about this axis is given by
IO′=IAB+ICD
Putting (1) and (2) in the above equation we get
IO′=12ml2+12ml2
⇒IO′=6ml2 ............................(3)
Now, we know that the moment of inertia of a ring about the axis passing through its centre and perpendicular to its plane is given by
I=MR2
According to the question, the mass of the ring is equal to m and its radius is equal to l/2 . Therefore substituting M=m and R=2l in the above equation, we get the moment of inertia of the given ring about the o-axis as
IO′′=4ml2 ............................(4)
Adding (4) and (5) we get the total moment of inertia of the system about the o-axis as
IO=6ml2+4ml2
⇒IO=125ml2 ............................(5)
Now, let us consider an axis x’y’ perpendicular to the xy axis, as shown in the below figure.
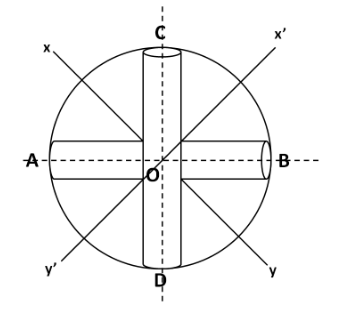
Let the moment of inertia of the system about the x’y’ axis be Ix′y′ . By symmetry, we can say that
Ix′y′=Ixy
By perpendicular axis theorem, we have
IO=Ixy+Ix′y′
⇒IO=2Ixy
Putting (5) in the above equation, we get
125ml2=2Ixy
⇒Ixy=245ml2
Thus, the moment of inertia of the system about the angle bisector is equal to 245ml2 .
Hence, the correct answer is option D.
Note
Do not forget to include the moment of inertia of the ring while calculating the moment of inertia of the system. The ring has a finite mass. So it will contribute to the moment of inertia of the system.
