Question

AB and CD are fixed conducting smooth rails placed in a vertical plane and joined by a constant current source at its upper end. PQ is a conducting rod which is free to slide on the rails. A horizontal uniform magnetic field exists in space as shown. If the rod PQ is released from rest, then:

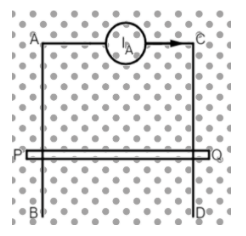
A. The rod PQ will move downward with constant acceleration
B. The rod PQ will move upward with constant acceleration
C. The rod PQ will remain at rest
D. Any of the above

Answer 1

Firstly, determine the forces that the rod PQ is subjected to, due to its mass, and due to the presence of the magnetic field. You can use Fleming’s Left Hand Rule to determine the direction of the magnetic force acting on the rod PQ, given the direction of the magnetic field and the direction of current flow. To this end, deduce the nature of motion of the rod under the influence of the combination of both gravitational and magnetic forces.

Formula Used:
$F_{gravitational} = mg$
$F_{magnetic} = iBl$

Complete Step-by-Step Solution:
We are given that the space contains a horizontal magnetic field. Let this be $\vec{B}$ that is directed into the plane of the paper. We also have moving charges or a constant current source $I_A$ directed as shown in the diagram. Let the length of the conducting rod PQ be $l$. In such a case, the current source and the magnetic field give rise to a magnetic force that acts on the rod, given as:
$F_{magnetic} = (\vec{I} \times \vec{B})l$.

The direction of this force can be deduced by Fleming's Left Hand rule, from which we get that the magnetic force on the rod acts vertically upwards.

Now, since the rod PQ is free to slide on the rails, this means that it slides either with or against gravity with some acceleration a. Since the rod possesses a mass, say m, it experiences a gravitational force subject to the acceleration due to gravity, g, given as:
$F_{gravitational}=mg$.

This force is directed vertically downwards.

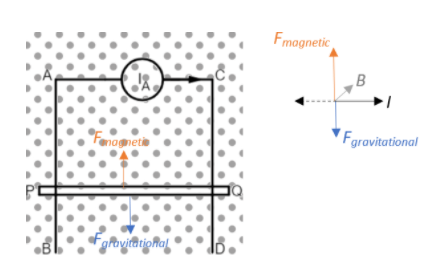
Now, from the diagram we can easily deduce that:
When $F_{gravitational} > F_{magnetic}$, the rod moves downwards in the direction of gravity with a net force equivalent to the difference between the two forces, i.e.,
$ma=mg-iBl$. Since $mg > iBl$, the net force, and the consequently the acceleration of the rod is directed downwards, and the value of acceleration will be $+ve$.

When $F_{gravitational} < F_{magnetic}$, the rod moves upwards against gravity with a net force equivalent to the difference between the two forces, i.e.,
$ma=mg-iBl$. Since $mg < iBl$, the net force, and consequently the acceleration of the rod is directed upwards, and the value of acceleration will be $-ve$.

Now suppose $F_{gravitational} = F_{magnetic}$. Then in such a case,
$ma=mg-iBl$. Since $mg = iBl \Rightarrow a=0$, there will be no acceleration and the rod remains at rest.

Thus, depending on the magnitude of gravitational and magnetic forces acting on the rod, it can either constantly accelerate upwards, downwards or remain at rest.

Therefore, the correct option would be D. Any of the above.

Note:
Remember that according to Fleming’s Lefthand Rule, if the thumb, index and the middle fingers are stretched out perpendicular to each other, then the thumb aligns with the direction of force acting on the conductor, the index finger aligns with the direction of the applied magnetic field, and the middle finger gives the current flowing through the conductor. Thus, by knowing the direction of any two of the above quantities, the direction of the third can be easily determined.
Also, do not forget that the force acting on the conductor is always perpendicular to the plane containing the current and the applied magnetic field vectors, which is indicated by the cross product between current I and applied field B : $F = (\vec{I} \times \vec{B})l$.