Question

$ab = ac \nRightarrow b-c$ $\Rightarrow ab-bc = 0$ $\Rightarrow b(a-c)=0$ $\Rightarrow b=0$ or $(a-c) \ge 0$ Do not cancel the terms from both sides, we can cancel only, If a is non zero.

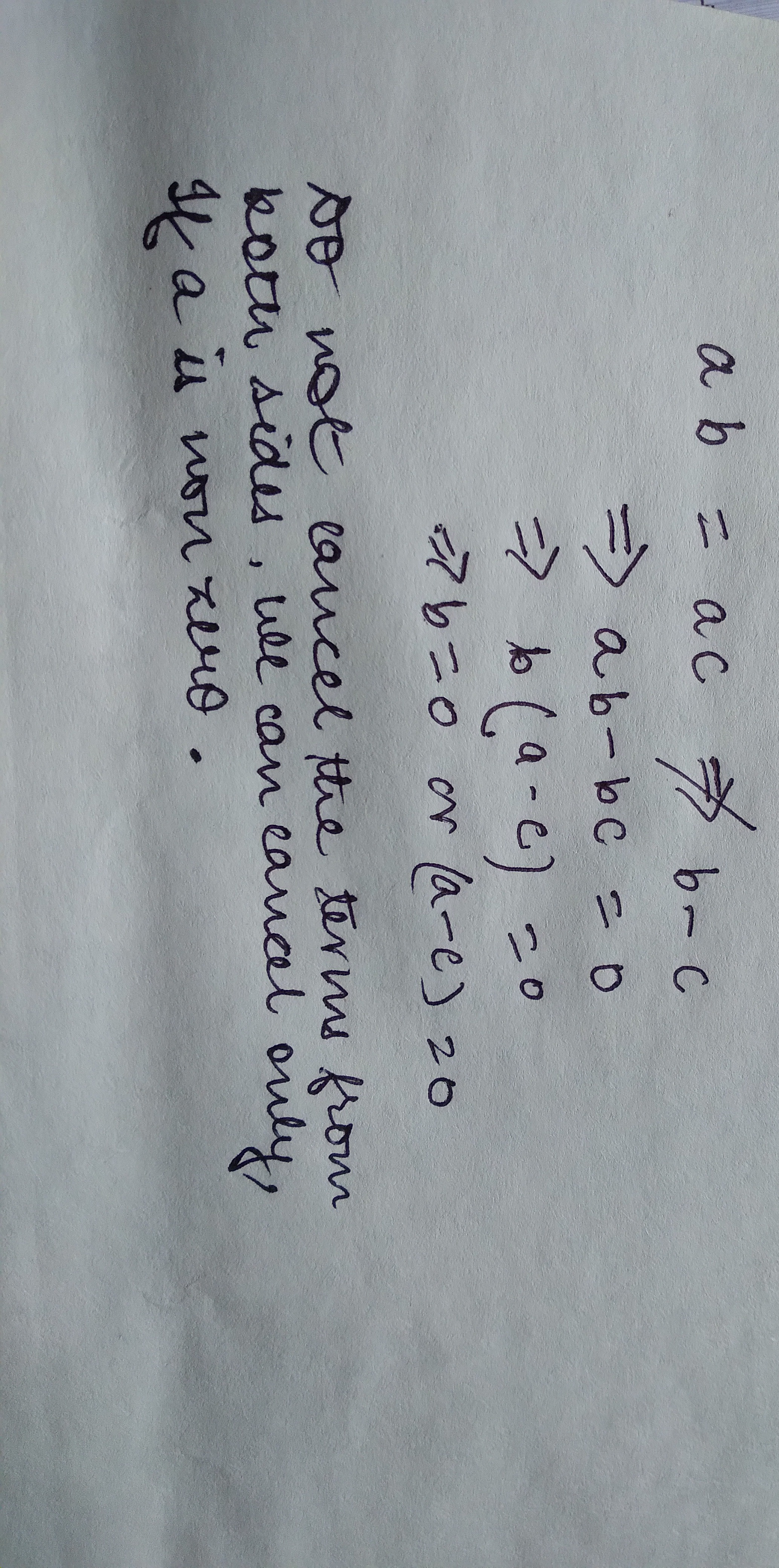
• A. If $ab=ac$, then $b=c$ unless $a=0$. In this case, $b$ and $c$ can be any value.
• B. The statement implies that if $a$ is non-zero, then $b$ must equal $c$.
• C. The reasoning provided ($ab-bc = 0 \Rightarrow b(a-c)=0 \Rightarrow b=0$ or $(a-c) \ge 0$) is correct.
• D. If $ab=ac$, it implies $b=c$ because we can always cancel $a$ from both sides.

Answer 1

Answer: (A)

If $ab=ac$, then $b=c$ unless $a=0$. In this case, $b$ and $c$ can be any value.

Answer 2

The initial equation is $ab = ac$. To understand the relationship between $b$ and $c$, we can rearrange the equation: $ab - ac = 0$ Factor out the common term $a$: $a(b-c) = 0$ For the product of two terms to be zero, at least one of the terms must be zero. Therefore, we have two possibilities:

1. $a = 0$
2. $b-c = 0 \Rightarrow b=c$

The note "Do not cancel the terms from both sides, we can cancel only, If a is non zero" is crucial. If $a \neq 0$, we can divide both sides of $a(b-c) = 0$ by $a$, which results in $b-c = 0$, thus $b=c$. However, if $a = 0$, the equation becomes $0 \cdot (b-c) = 0$, which simplifies to $0 = 0$. This equation is true for any values of $b$ and $c$. Therefore, if $a=0$, $b$ is not necessarily equal to $c$.

The provided reasoning "$ab-bc = 0 \Rightarrow b(a-c)=0 \Rightarrow b=0$ or $(a-c) \ge 0$" contains errors:

• The step "$ab-bc = 0$" is incorrect if the starting point is $ab=ac$. It should be $ab-ac=0$.
• The step "$b(a-c)=0$" would follow from $ab-bc=0$, but not from $ab=ac$.
• The conclusion "$b=0$ or $(a-c) \ge 0$" is incorrect. From $b(a-c)=0$, the correct conclusion is $b=0$ or $a-c=0$. The condition $(a-c) \ge 0$ is not implied.

Thus, the statement $ab=ac$ implies $b=c$ only if $a$ is non-zero. If $a=0$, $b$ and $c$ can be any values.