Question

A Young's double slit interference arrangement with slits ${{S}_{1}}$ and ${{S}_{2}}$ is immersed in water (refractive index $=\dfrac{4}{3}$) as shown in the figure. The positions of maxima on the surface of water are given by ${{x}^{2}}={{p}^{2}}{{m}^{2}}{{\lambda }^{2}}-{{d}^{2}}$, where ‘$\lambda$’ is the wavelength of light in air (refractive index = 1), 2d is the separation between the slits and m is an integer. The value of P is____

Answer 1

We are given a Young’s double slit experiment with one of the slits immersed in water. It is said that a maxima is formed on the surface of water and we are given the equation of this position. We can draw the path of the maxima and find its path difference. Thus we can find the equation of the maxima and by comparing it with the given equation we can find the required solution.

Formula used:
$\text{time=}\dfrac{\text{distance}}{\text{velocity}}$
$n=\dfrac{c}{v}$
$\Delta x=m\lambda$

Complete step-by-step answer:
In the question we are given a Young’s double slit experiment where the slit is immersed in water.
The refractive index of water is given to us as $\dfrac{4}{3}$.
It is said that a maxima is formed on the surface.
The figure given below will show the maxima formed.

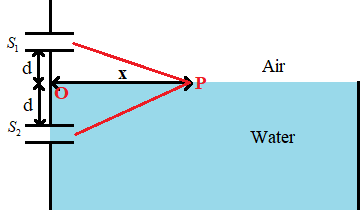
From the figure we can see that the path traveled by the light from the slit ${{S}_{1}}$ is
${{S}_{1}}P$.
From the right angled triangle in the figure, ${{S}_{1}}PO$, we can see that the side
${{S}_{1}}{{P}^{2}}={{S}_{1}}{{O}^{2}}+O{{P}^{2}}$
Since ${{S}_{1}}O=d$ and $OP=x$, we get
$\Rightarrow {{S}_{1}}{{P}^{2}}={{d}^{2}}+{{x}^{2}}$
Therefore we have,
$\Rightarrow {{S}_{1}}P=\sqrt{{{d}^{2}}+{{x}^{2}}}$
We know that the time taken to travel this distance is given by,
$\text{time=}\dfrac{\text{distance}}{\text{velocity}}$
Therefore here,
$\Rightarrow T=\dfrac{{{S}_{1}}P}{v}$
We know that refractive index is given by the formula,
$n=\dfrac{c}{v}$, were ‘c’ is the velocity of light in vacuum and ‘v’ is the velocity of light in the medium.
Here we know that the refractive index of air is 1. Therefore we can write,
$\Rightarrow \dfrac{c}{v}=1$
From this we get the velocity in the medium as,
$\Rightarrow v=c$
Therefore the time taken to travel the path ${{S}_{1}}P$ will be,
$\Rightarrow T=\dfrac{{{S}_{1}}P}{c}$
$\Rightarrow Tc={{S}_{1}}P$
Therefore the total distance traveled by the light is,
$\Rightarrow Tc={{S}_{1}}P=\sqrt{{{d}^{2}}+{{x}^{2}}}$
In the case of the light coming from ‘${{S}_{2}}$’ from the figure we can see that the path is ${{S}_{2}}P$ which is,
${{S}_{2}}P=\sqrt{{{d}_{2}}+{{x}_{2}}}$
As in the above case, the time taken by the light to travel can be written as,
$T=\dfrac{{{S}_{2}}P}{v}$
We also know that the refractive index, $n=\dfrac{c}{v}$
The refractive index of water is given as $\dfrac{4}{3}$. Therefore we get,
$\Rightarrow \dfrac{c}{v}=\dfrac{4}{3}$
From this equation we get the velocity of light in the medium as,
$\Rightarrow v=\dfrac{3}{4}c$
Therefore the time taken will be,
$\Rightarrow T=\dfrac{{{S}_{1}}P}{\left( \dfrac{3}{4}c \right)}$
$\Rightarrow T=\dfrac{4{{S}_{1}}P}{3c}$
$\Rightarrow T=\dfrac{4}{3c}\sqrt{{{d}^{2}}+{{x}^{2}}}$
Hence we get the total distance traveled by the light in water medium as,
$\Rightarrow Tc=\dfrac{4}{3}\sqrt{{{d}^{2}}+{{x}^{2}}}$
This is the optical path of the light (path traveled by light in a medium).
We know that there is a path difference in the path of the light in air and water.
This path difference is,
$\Delta x=\left( \dfrac{4}{3}\sqrt{{{d}^{2}}+{{x}^{2}}} \right)-\left( \dfrac{4}{3}\sqrt{{{d}^{2}}+{{x}^{2}}} \right)$
$\Rightarrow \Delta x=\left( \sqrt{{{d}^{2}}+{{x}^{2}}} \right)\left( \dfrac{4}{3}-1 \right)$
$\Rightarrow \Delta x=\dfrac{1}{3}\left( \sqrt{{{d}^{2}}+{{x}^{2}}} \right)$
We know that the maxima at the surface will be equal to the wavelength of the light multiplied by an integer, i.e.
$\Delta x=m\lambda$
$\Rightarrow \dfrac{1}{3}\left( \sqrt{{{d}^{2}}+{{x}^{2}}} \right)=m\lambda$
On squaring both sides, we get
$\Rightarrow \dfrac{1}{9}\left( {{d}^{2}}+{{x}^{2}} \right)={{m}^{2}}{{\lambda }^{2}}$
By solving this we get,
$\Rightarrow {{d}^{2}}+{{x}^{2}}=9{{m}^{2}}{{\lambda }^{2}}$
$\Rightarrow {{x}^{2}}=9{{m}^{2}}{{\lambda }^{2}}-{{d}^{2}}$
In the question we are given that the position of maxima on the surface is,
${{x}^{2}}={{p}^{2}}{{m}^{2}}{{\lambda }^{2}}-{{d}^{2}}$
By comparing these two equations, we get
$\Rightarrow {{p}^{2}}=9$
$\Rightarrow p=\sqrt{9}=3$
Therefore we get the value of p as 3.

Note: In the question we are performing a Young’s double slit experiment. This experiment helps us to understand the wave theory of light. Young’s double slit experiment demonstrates the constructive and destructive interference pattern of light.
Interference is a phenomenon where two waves superimpose together and form a new wave which may have greater, lower or the same amplitude of the interfering waves.