Question

Triangle ABC is right angled at A. The circle with centre A and radius AB cuts BC and AC internally at D and E respectively. If BD = 20 and DC = 16 then the length AC equals

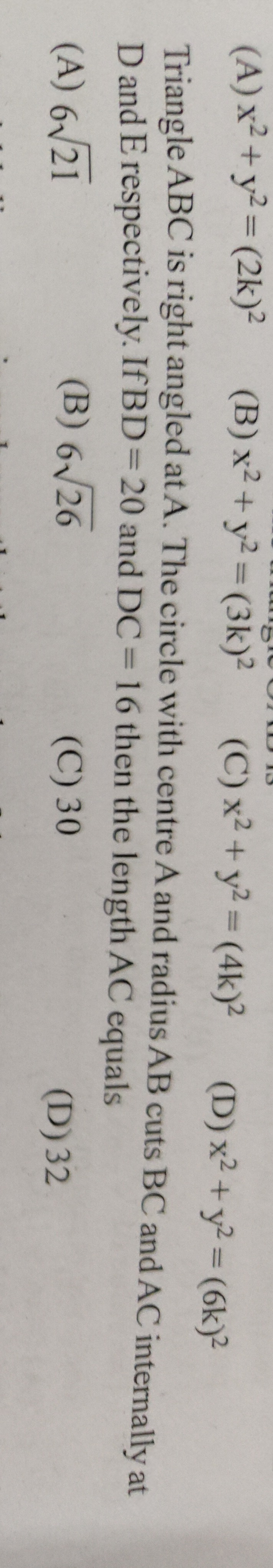
• A. 6√21
• B. 6√26
• C. 30
• D. 32

Answer 1

Answer: (B)

6√26

Answer 2

In right-angled triangle ABC, let AB = b and AC = c. Given BD = 20 and DC = 16, so BC = BD + DC = 20 + 16 = 36. By the Pythagorean theorem in $\triangle ABC$: $AB^2 + AC^2 = BC^2$ $b^2 + c^2 = 36^2 = 1296$ (Equation 1)

The circle with center A and radius AB cuts BC at D and AC at E. This means AD = AB = b and AE = AB = b.

In $\triangle ABC$, the cosine of angle C is given by $\cos C = \frac{AC}{BC} = \frac{c}{36}$.

Now, consider $\triangle ADC$. By the Law of Cosines: $AD^2 = AC^2 + DC^2 - 2(AC)(DC)\cos C$ Substitute the known values: $b^2 = c^2 + 16^2 - 2(c)(16)\left(\frac{c}{36}\right)$ $b^2 = c^2 + 256 - \frac{32c^2}{36}$ $b^2 = c^2 + 256 - \frac{8c^2}{9}$

To eliminate the fraction, multiply the entire equation by 9: $9b^2 = 9c^2 + 9(256) - 8c^2$ $9b^2 = c^2 + 2304$ (Equation 2)

Now we have a system of two equations with two variables ($b^2$ and $c^2$):

1. $b^2 + c^2 = 1296$
2. $9b^2 = c^2 + 2304$

From Equation 1, we can express $b^2$ as $b^2 = 1296 - c^2$. Substitute this expression for $b^2$ into Equation 2: $9(1296 - c^2) = c^2 + 2304$ $11664 - 9c^2 = c^2 + 2304$

Rearrange the terms to solve for $c^2$: $11664 - 2304 = c^2 + 9c^2$ $9360 = 10c^2$ $c^2 = \frac{9360}{10} = 936$

The length of AC is c. So, $AC = \sqrt{936}$. To simplify $\sqrt{936}$: $936 = 36 \times 26$ $AC = \sqrt{36 \times 26} = \sqrt{36} \times \sqrt{26} = 6\sqrt{26}$.