Question

(a). Write the principle of working on a meter bridge.
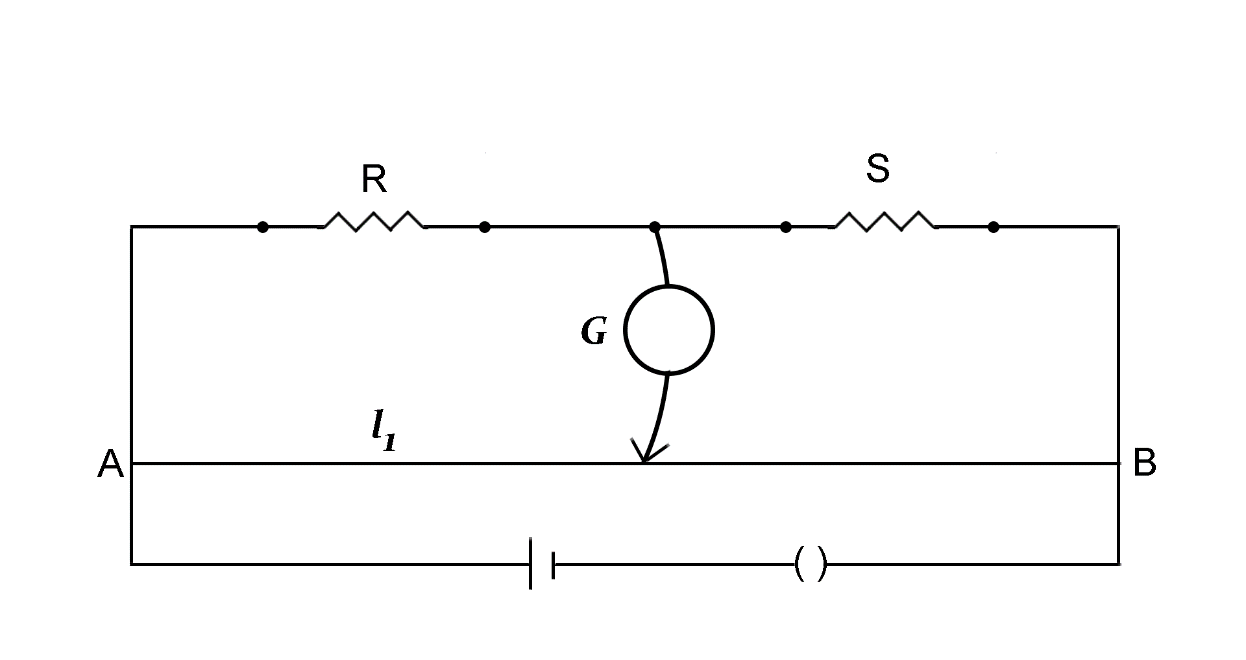
(b). In a meter bridge, the balance point is found at a distance ${l_1}$ with resistance $R$ and $S$ as shown in the figure. An unknown resistance $X$ is now connected in parallel to the resistance $S$ and the balance point is found at a distance ${l_2}$ . Obtain a formula for $X$ in terms of ${l_1}$ , ${l_2}$ and $S$ .

Answer 1

- Hint: You can start by defining the principle behind Meter Bridge (the concept of wheatstone bridge). Then use the equation $\dfrac{R}{S} = \dfrac{{{l_1}}}{{100 - {l_1}}}$ on the circuit before and after connecting the resistance $X$ in parallel. Compare the equations to reach the solution.

Complete step-by-step answer:
(a). Meter Bridge is also known as a slide wire bridge. Meter Bridge is a practical form of wheatstone bridge. A wire of $1m(100cm)$ and uniform area of cross-section is made up of constantan or manganin. This wire is stretched between two strips made up of copper which holds the wire in place.
According to the concept of wheatstone bridge circuit, any point on the wire the ratio of two resistors (in this case $R$ and $S$ ) is equal to the ration of the resistance of the wire of any length (in this case ${l_1}$ ) and the resistance of the remaining wire (in this case $100 - {l_1}$ ).
(b). In the given problem we have two resistors $R$ and $S$ . The pointer is set at a point where it divides the $100cm$ into different segments: one of ${l_1}cm$ length and one of $100 - {l_1}cm$ length.
So using the concept of wheatstone bridge, we get
$\dfrac{R}{S} = \dfrac{{{l_1}}}{{100 - {l_1}}}$
$R = \dfrac{{S{l_1}}}{{100 - {l_1}}}$
When we connect a resistance $X$ in parallel to $S$ , we have the following circuit.

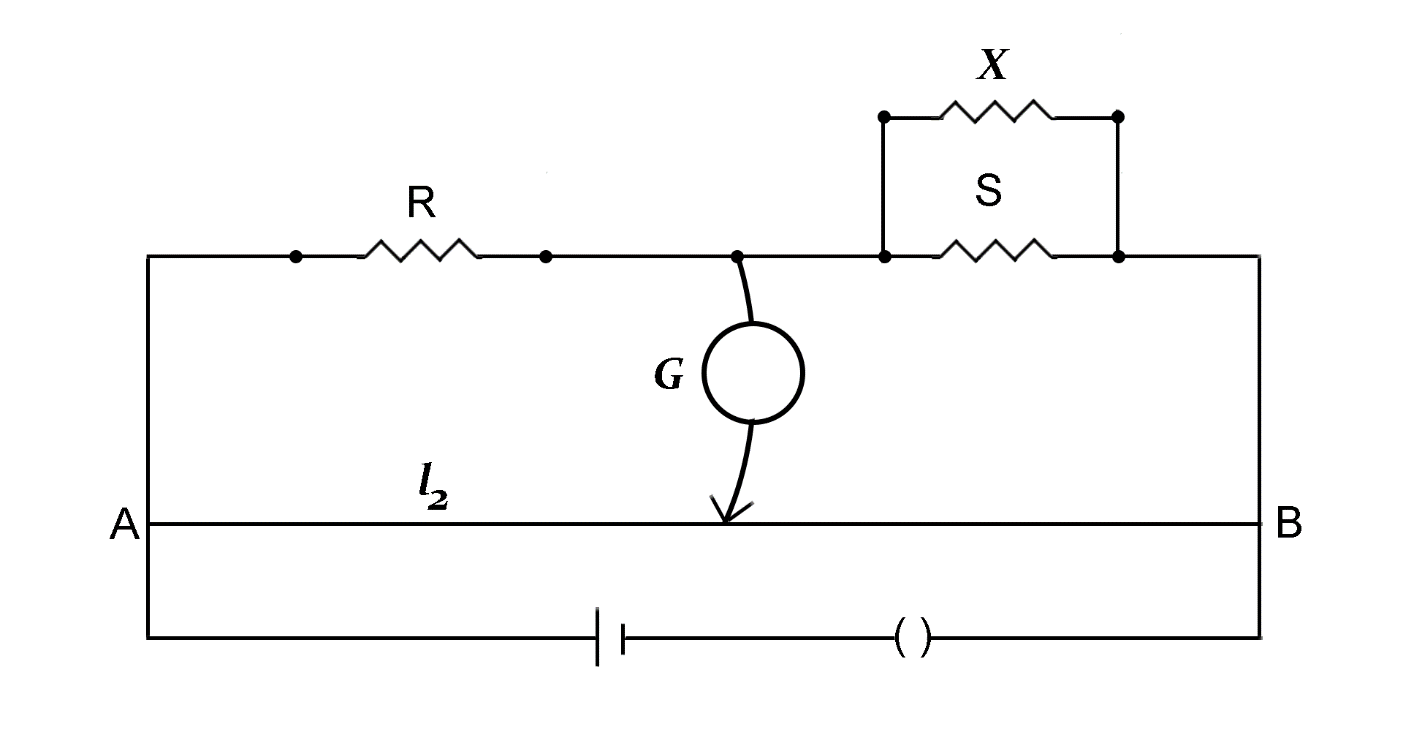
Let’s assume that $X$ and $S$ resistors in parallel produce a combined resistance of $Z$.
$Z = \dfrac{{SX}}{{S + X}}$
Now, again using the concept of wheatstone, we get
$\dfrac{R}{Z} = \dfrac{{{l_2}}}{{100 - {l_2}}}$
Substituting $R$and$Z$
$\dfrac{{S{l_1}}}{{100 - {l_1}}} \times \dfrac{{S + X}}{{SX}} = \dfrac{{{l_2}}}{{100 - {l_2}}}$
$\Rightarrow (100 - {l_2}){l_1}(S + X) = (100 - {l_1}){l_2}X$
$\Rightarrow X = \dfrac{{{l_1}S(100 - {l_2})}}{{100({l_2} - {l_1})}}$

Note: Wheatstone bridge is essentially an electric circuit that is in the form of a bridge. The two sides of the bridge are connected by a galvanometer. The wheatstone bridge is named after Sir Charles wheatstone who helped in popularizing it. It helps in calculating the resistance of an unknown resistance.