Question
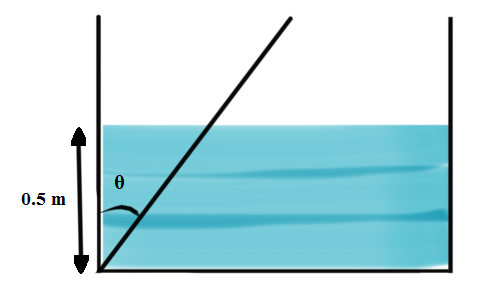
Question: A wooden plank of length 1 m and uniform cross section is hinged at one end to the bottom of a tank ...
A wooden plank of length 1 m and uniform cross section is hinged at one end to the bottom of a tank as shown in figure. The tank is filled with water up to a height of 0.5 m. The specific gravity of the plank is 0.5. Find the angle θ (in degrees) that the plank makes with the vertical in the equilibrium position (exclude the case θ = 0).
Solution
The plank is hinged and is free to rotate about the axis. In equilibrium of the wooden plank beneath the water, it will experience no torture. The equilibrium is caused by the balance of force downwards due to its weight and a force upwards due to the water (buoyant force).
Formula used:
Torque acting on an endpoint at a distance r from the axis of a rod l is;
τ=F.r.sinθ
Where F is the magnitude of force acting at that point and θ is the angle between F and r directions.
Complete answer:
Assume that the plank has a length x m above the water and a length (1-x) m below the surface of the water.
When an object is placed in the water, the buoyant force acting on it is equal to the weight of the water displaced by the body. The (volume of the) wooden plank beneath the surface will cause this force. Therefore the buoyant force acting upwards will become m′gsinθ. So the torque upwards will be:
τup=ρ0.(1−x).A.g.21−xsinθ
Where A is a uniform cross section of the plank.
Gravity is a central force so it acts from the centre of the rod i.e., the rod exerts mg downwards at a distance of 1/2 m or 0.5 m (centre of the rod).
Therefore downward force becomes mg where we can write density x volume in place of mass.
So the torque can be written as:
τdown=ρ.1.A.g.0.5.sinθ
We are given that Specific gravity or the relative density of the wooden plank is 0.5. Relative density is the ratio of the density of an object divided by the density of water. Therefore, the density of wooden planks becomes 0.5×ρ0.
We may write:
τdown=0.5.ρ0A.g.0.5.sinθ
Equating the magnitudes of two opposing torques, we get:
ρ0A.g.2(1−x)2sinθ=(0.5)2.ρ0A.g.sinθ
Simplification of this produces:
2(1−x)2=(0.5)2
Or, we can write:
(1−x)2=0.5
gives us x= 0.29 m.
But we only need the value of (1-x) = 0.707 which is the length of the submerged plank making an angle θ. Therefore, from the right angled triangle, we get
cosθ=0.7070.5
⟹cosθ=0.707
Taking cos-1 on both sides gives us the angle as:
θ=44.99∘
Therefore, we can say that the plank makes an angle of about 45∘.
Note:
While noting down the buoyant force one should take care of the fact that only a part of the length of the plank is submerged inside the water. Therefore we wrote (1-x)m instead of 1 m when writing the volume of the water displaced. The volume of the water displaced is equal to the volume of wooden plank under water, only the densities differ for the two.
