Question

A wooden box is placed on a table. The normal force on the box from the table is$N_1$. Now another identical box is kept on the first box and the normal force on the lower block due to the upper block is $N_2$ and normal force on the lower block by the table is $N_3$. For this situation, mark the correct option:
$\text{A.}\quad N_1 = N_2 = N_3$
$\text{B.}\quad N_1 < N_2 = N_3$
$\text{C.}\quad N_1 = N_2 < N_3$
$\text{D.}\quad N_1 = N_2 > N_3$

Answer 1

Normal force is a type of force acting normal to the surface on an object having contact with the surface. This is called normal force as it acts in the direction of normal to the surface. This reason for normal force is that when gravity applies force on an object, there has to be some force, which is balancing the gravitational force, we call it normal reaction. This is the reason why if a block is placed on the table, why it doesn't start moving, in spite of gravity acting on it.

Complete answer:
Let’s first analyze the situation mathematically. The two blocks are identical, hence let the mass of both be ’$m$’ each. Now, in the case when only one block is placed on the table, we can see by free body diagram 1, that in equilibrium conditions, normal ($N_1$) balances the weight.

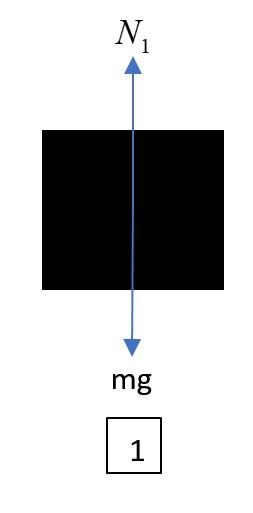
Thus $N_1 = mg$
Now, when an identical block is placed on the first block, the net force on the block placed should also be zero. Hence again normal ($N_2$) balances the weight (mg) of the block, as shown in figure 2.

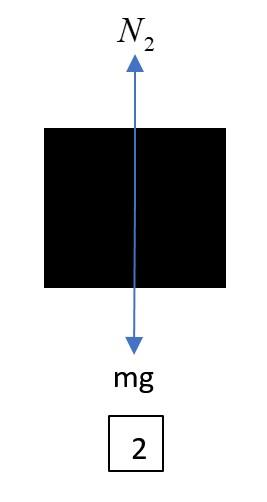
$N_2 = mg$
Finally, in the staked condition, we can see for the two block system, the net force on the system is zero (not accelerated). Hence normal($N_3$) will balance the whole weight(2mg) of the system.

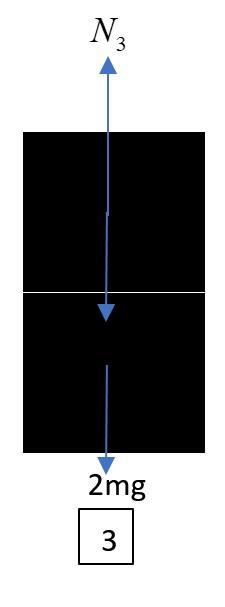
$N_3=mg+mg=2mg$
Thus, $N_1 = N_2 < N_3$

So, the correct answer is “Option C”.

Note:
These types of questions can be easily solved by drawing the free body diagram of the individual blocks and analyzing the equilibrium conditions. One must point out that in figure 2, if the lower block applies force ($N_2$) on the upper block then for validating Newton’s $3^{rd}$ law of motion, the upper block will also apply force on the lower block, thereby increasing the normal. Well, Newton's law is perfectly valid everywhere, it’s just that normal reaction between the blocks is internal force, which don’t constitute in each other’s normal reactions.