Question

A woman weighing 50kg stands on a weighing machine placed in a lift. What will be the reading of the machine, when the lift is (i) moving upwards with a uniform velocity of $5\,{\text{m}} \cdot {{\text{s}}^{ - 1}}$ and (ii) moving downwards with a uniform acceleration of $1\,{\text{m}} \cdot {{\text{s}}^{ - 2}}$. Take $g = 10\,{\text{m}} \cdot {{\text{s}}^{ - 2}}$.

Answer 1

Use the expression for Newton’s second law of motion. Draw the free body diagram of the woman for both the cases and apply Newton’s second law of motion to the woman in the vertical direction considering proper directions of the forces on the woman and proper signs.

Formulae used:
The expression for Newton’s second law of motion is
${F_{net}} = ma$
Here, ${F_{net}}$ is the net force on the object, $m$ is the mass of the object and $a$ is the acceleration of the object.

Complete step by step answer:
We have given that the weight of the woman standing on the weighing machine is $50\,{\text{kg}}$.

(i) Let $m$ be the mass of the woman.
$m = 50\,{\text{kg}}$

It is given that the lift is moving upward with a uniform velocity of $5\,{\text{m}} \cdot {{\text{s}}^{ - 1}}$.

Draw the free-body diagram of the woman.

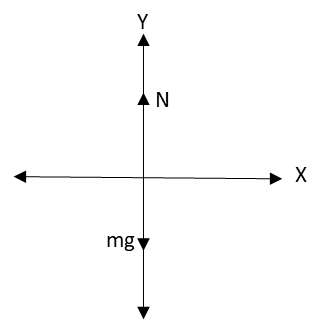
In the above diagram, $N$ is the normal force on the woman by the lift and $mg$ is the weight of the woman.

The weight measured by the machine is equal to the normal force.

Apply Newton’s second law of motion to the woman.
$N - mg = ma$

Since the lift is moving upward with a uniform velocity, the acceleration of the lift will be zero.

Substitute $0\,{\text{m/}}{{\text{s}}^2}$ for $a$ in the above equation.
$N - mg = m\left( {0\,{\text{m/}}{{\text{s}}^2}} \right)$
$\Rightarrow N = mg$

Substitute $50\,{\text{kg}}$ for $m$ and $10\,{\text{m}} \cdot {{\text{s}}^{ - 2}}$ for $g$ in the above equation.
$N = \left( {50\,{\text{kg}}} \right)\left( {10\,{\text{m}} \cdot {{\text{s}}^{ - 2}}} \right)$
$\Rightarrow N = 500\,{\text{N}}$

Hence, the reading of the machine when the lift is moving upward is $500\,{\text{N}}$.

(ii) Now the lift is moving downward with an acceleration of $1\,{\text{m}} \cdot {{\text{s}}^{ - 2}}$.

Draw the free-body diagram of the woman.

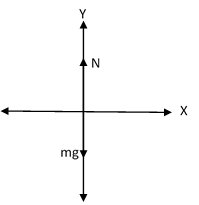
Apply Newton’s second law of motion to the woman.
$N - mg = - ma$
$\Rightarrow N = m\left( {g - a} \right)$

Substitute $50\,{\text{kg}}$ for $m$, $10\,{\text{m}} \cdot {{\text{s}}^{ - 2}}$ for $g$ and $1\,{\text{m}} \cdot {{\text{s}}^{ - 2}}$ for $a$ in the above equation.
$\Rightarrow N = \left( {50\,{\text{kg}}} \right)\left( {10\,{\text{m}} \cdot {{\text{s}}^{ - 2}} - 1\,{\text{m}} \cdot {{\text{s}}^{ - 2}}} \right)$
$\Rightarrow N = 450\,{\text{N}}$

Hence, the reading of the machine when the lift is moving downward is $450\,{\text{N}}$.

Note:
While applying Newton’s second law of motion to the woman, use the proper signs of the forces and acceleration as the acceleration in the first case is in upward direction and in the second case, the acceleration is in downward direction. The students might get confused as to how normal force measures the weight of women. But the normal force balances the net remaining force on the woman, hence, it gives the reading shown by the machine.