Question

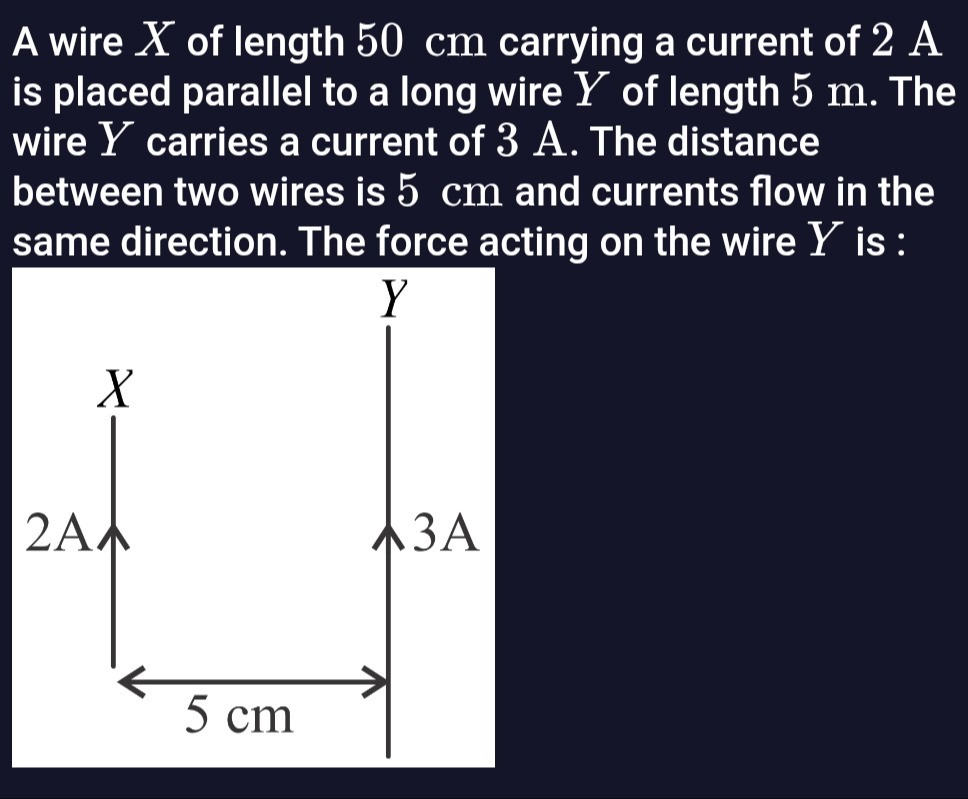
A wire $X$ of length 50 cm carrying a current of 2 A is placed parallel to a long wire $Y$ of length 5 m. The wire $Y$ carries a current of 3 A. The distance between two wires is 5 cm and currents flow in the same direction. The force acting on the wire $Y$ is :

• A. 1.2 x 10^-5 N attractive
• B. 1.2 x 10^-4 N attractive
• C. 1.2 x 10^-5 N repulsive
• D. 1.2 x 10^-4 N repulsive

Answer 1

Answer: (A)

1.2 x 10^-5 N attractive

Answer 2

The force between two parallel wires carrying currents $I_1$ and $I_2$ separated by a distance $d$ is given by the formula for force per unit length: $\frac{F}{l} = \frac{\mu_0 I_1 I_2}{2 \pi d}$ The force is attractive if the currents are in the same direction and repulsive if they are in opposite directions.

Given: Length of wire X, $l_X = 50$ cm $= 0.5$ m. Current in wire X, $I_X = 2$ A. Length of wire Y, $l_Y = 5$ m. Current in wire Y, $I_Y = 3$ A. Distance between the wires, $d = 5$ cm $= 0.05$ m. The currents flow in the same direction, so the force is attractive.

When calculating the force between two parallel wires of finite lengths, the interaction length is typically limited by the shorter wire, as the magnetic field of the longer wire is approximately uniform over the length of the shorter wire. Here, wire X is shorter ($l_X = 0.5$ m). Therefore, the interaction length $l$ to be used in the force formula is $l_X = 0.5$ m.

The magnitude of the force is given by: $F = \frac{\mu_0 I_X I_Y l}{2 \pi d}$ Using the value of $\mu_0 = 4\pi \times 10^{-7}$ T m/A: $F = \frac{(4\pi \times 10^{-7} \text{ T m/A}) (2 \text{ A}) (3 \text{ A}) (0.5 \text{ m})}{2 \pi (0.05 \text{ m})}$ $F = \frac{2 \times 10^{-7} \times 6 \times 0.5}{0.05} \text{ N}$ $F = \frac{6 \times 10^{-7}}{0.05} \text{ N}$ $F = \frac{600 \times 10^{-7}}{5} \text{ N}$ $F = 120 \times 10^{-7} \text{ N}$ $F = 1.2 \times 10^{-5} \text{ N}$

By Newton's third law, the force acting on wire Y due to wire X is equal in magnitude to the force acting on wire X due to wire Y. Since the currents are in the same direction, the force is attractive.

Therefore, the force acting on wire Y is $1.2 \times 10^{-5}$ N attractive.