Question

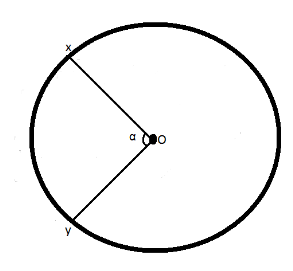
A wire of resistance $R$ is bent into a circular ring of radius $r$ . Equivalent resistance between two points $x$ and $y$ on its circumferences, when angle $XOY$ is $\alpha$ , can be given by:

\left( A \right)\dfrac{{R\alpha }}{{4{\pi ^2}}}\left( {2\pi - \alpha } \right) \\\ \left( B \right)\dfrac{{R\alpha }}{{2\pi }}\left( {2\pi - \alpha } \right) \\\ \left( C \right)R\left( {2\pi - \alpha } \right) \\\ \left( D \right)\dfrac{{4\pi }}{{R\alpha }}\left( {2\pi - \alpha } \right) \\\

Answer 1

Hint : In this question, we are going to first take two points $z$ and $w$ , in the different sections to define them easily, then the resistances for both of them are calculated from the resistance per unit length, and then as they are in parallel combination, equivalent resistance is calculated.
The resistance of an element is given by,
${R_{xwy}} = Resistance{\text{ }}per{\text{ }}unit{\text{ }}length \times Length{\text{ }}of{\text{ }}the{\text{ }}element$
For two resistors ${R_1}$ and ${R_2}$ connected in parallel.

Complete Step By Step Answer:
As we know that the resistance of a wire is directly proportional to the length.
Now, taking the points $z$ and $w$ , on the wire as given in the diagram below

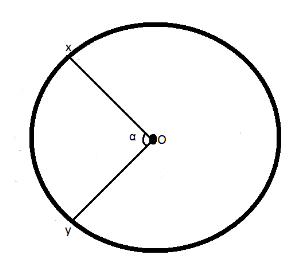
Let us take the element $xwy$ , the resistance is given by,
${R_{xwy}} = Resistance{\text{ }}per{\text{ }}unit{\text{ }}length \times Length{\text{ }}of{\text{ }}the{\text{ }}element$
Putting the values in this, we get
${R_{xwy}} = \dfrac{R}{{2\pi r}} \times r\alpha = \dfrac{{R\alpha }}{{2\pi }}$
Now taking the length element
${R_{xwy}} = \dfrac{R}{{2\pi r}} \times r\left( {2\pi - \alpha } \right) = \dfrac{{R\left( {2\pi - \alpha } \right)}}{{2\pi }}$
As we look at the elements, if they are considered to be two resistors connected to each other, then, this connection is in parallel. Now the equivalent resistance for this parallel combination is calculated as:
${R_{eq}} = \dfrac{{{R_{xwy}}{R_{xzy}}}}{{{R_{xwy}} + {R_{xzy}}}}$
Now putting the values of the resistances, as obtained above, we get
${R_{eq}} = \dfrac{{\dfrac{{R\left( {2\pi - \alpha } \right)}}{{2\pi }} \times \dfrac{{R\alpha }}{{2\pi }}}}{{\dfrac{{R\left( {2\pi - \alpha } \right)}}{{2\pi }} + \dfrac{{R\alpha }}{{2\pi }}}} = \dfrac{{R\alpha }}{{4{\pi ^2}}}\left( {2\pi - \alpha } \right)$
Hence, the option $\left( A \right)\dfrac{{R\alpha }}{{4{\pi ^2}}}\left( {2\pi - \alpha } \right)$ is the correct answer.

Note :
For two resistors to be connected in parallel, the current has to be divided between them depending upon their resistances while the voltage remains the same. As in this question, for the two elements of the wire, the current gets divided, depending upon the resistances, the voltage is the same for both.