Question

A wire of resistance $9\,\Omega$ is connected with the two batteries as shown in the adjoining circuit. The potential difference between the points A and B is:

A. $15\,{\text{V}}$
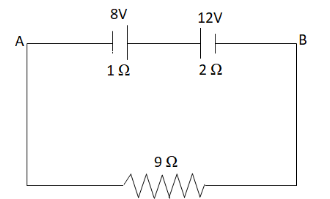
B. $- 15\,{\text{V}}$
C. $3\,{\text{V}}$
D. $- 3\,{\text{V}}$

Answer 1

To find the potential difference between the points A and B, we need to find the current flowing in the circuit. Here, we will need to apply Kirchhoff’s voltage law. Using this law, we can find the value of current flowing in the circuit and using this value of current we can find the potential difference between A and B.

Complete step by step answer:
Given, resistance of wire, $R = 9\Omega$
Emf of one battery, ${\varepsilon _1} = 8\,{\text{V}}$ and internal resistance, ${r_1} = 1\Omega$
Emf of other battery, ${\varepsilon _2} = 12\,{\text{V}}$ and internal resistance, ${r_2} = 2\,\Omega$
Let us assume current $i$ flows through the circuit.We draw a diagram to show the flow of current.

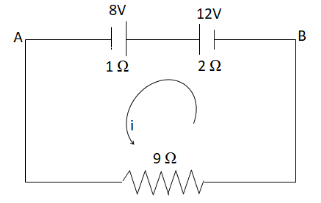
We will apply here Kirchhoff’s voltage law, according to which the algebraic sum of all the potential differences around any closed loop is equal to zero.The given circuit is a closed circuit, so we can use Kirchhoff’s voltage law and find the current in the circuit.
Applying Kirchhoff’s voltage law in the given circuit we get,
$2 \times i - 12 + 1 \times i + 8 + 9 \times i = 0$
$\Rightarrow 2i - 12 + i + 8 + 9i = 0$
$\Rightarrow 12i - 4 = 0$
$\Rightarrow i = \dfrac{4}{{12}}\,{\text{A}}$
Potential difference between two points is given by,
$V = IR$
where $I$ is the current flowing between the two points and $R$ is the resistance between the two points.
So, here potential difference between the points A and B will be
$V = iR$
Putting the value of $i$ and $R$ we get,
$V = \dfrac{4}{{12}} \times 9$
$\Rightarrow V = \dfrac{1}{3} \times 9$
$\therefore V = 3\,{\text{V}}$
Therefore, the potential difference between the points A and B is $3\,{\text{V}}$.

Hence, the correct answer is option C.

Note: There are two Kirchhoff’s laws. First is the Kirchhoff’s current law which states in a junction, total current entering the junction is equal to total current leaving the junction. Second is the Kirchhoff’s voltage law which we have discussed in the above question. For solving problems related to circuits, these two laws are very important.