Question

A wire of resistance $8\Omega$ is bent into a circle. Find the resistance across the diameter.

Answer 1

To solve this question, first we need to find the resistance of the two arcs of the semicircle. This can be easily calculated if we know the relation between the resistance of wire and length of wire. After that, we can calculate the resistance across the diameter if we know that the arcs are connected in parallel.

Formulae used:
$\dfrac{{{R_1}}}{{{l_1}}} = \dfrac{{{R_2}}}{{{l_2}}}$
Where ${R_1}$ and ${R_2}$ are the resistance of the wire and ${l_1}$ and ${l_2}$ are the length of the wire.
$\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$
Where ${R_1}$ and ${R_2}$ are the resistance connected in parallel, and $R$ is the net resistance of the wires connected in parallel.

Complete step by step answer:
In the question, the resistance of the wire is given to be $8\Omega$. Let the length of that wire be $l$.
It is said the wire was bent into a circle. So the length of the wire will be the circumference of the circle. Hence, the length of each half of the circle will be $\dfrac{l}{2}$.
So the resistance of the halves will be,
$\Rightarrow \dfrac{{{R_1}}}{{{l_1}}} = \dfrac{{{R_2}}}{{{l_2}}}$
Where ${R_1}$ and ${R_2}$ are the resistance of the wire and that of each half of the circle respectively and ${l_1}$ and ${l_2}$ are the length of the wire and each half of the circle respectively.
$\Rightarrow \dfrac{8}{l} = \dfrac{R}{{\dfrac{l}{2}}}$
$\Rightarrow R = 4\Omega$
So the resistance of each arc will be $4\Omega$. The arcs of the circle can be modified as,

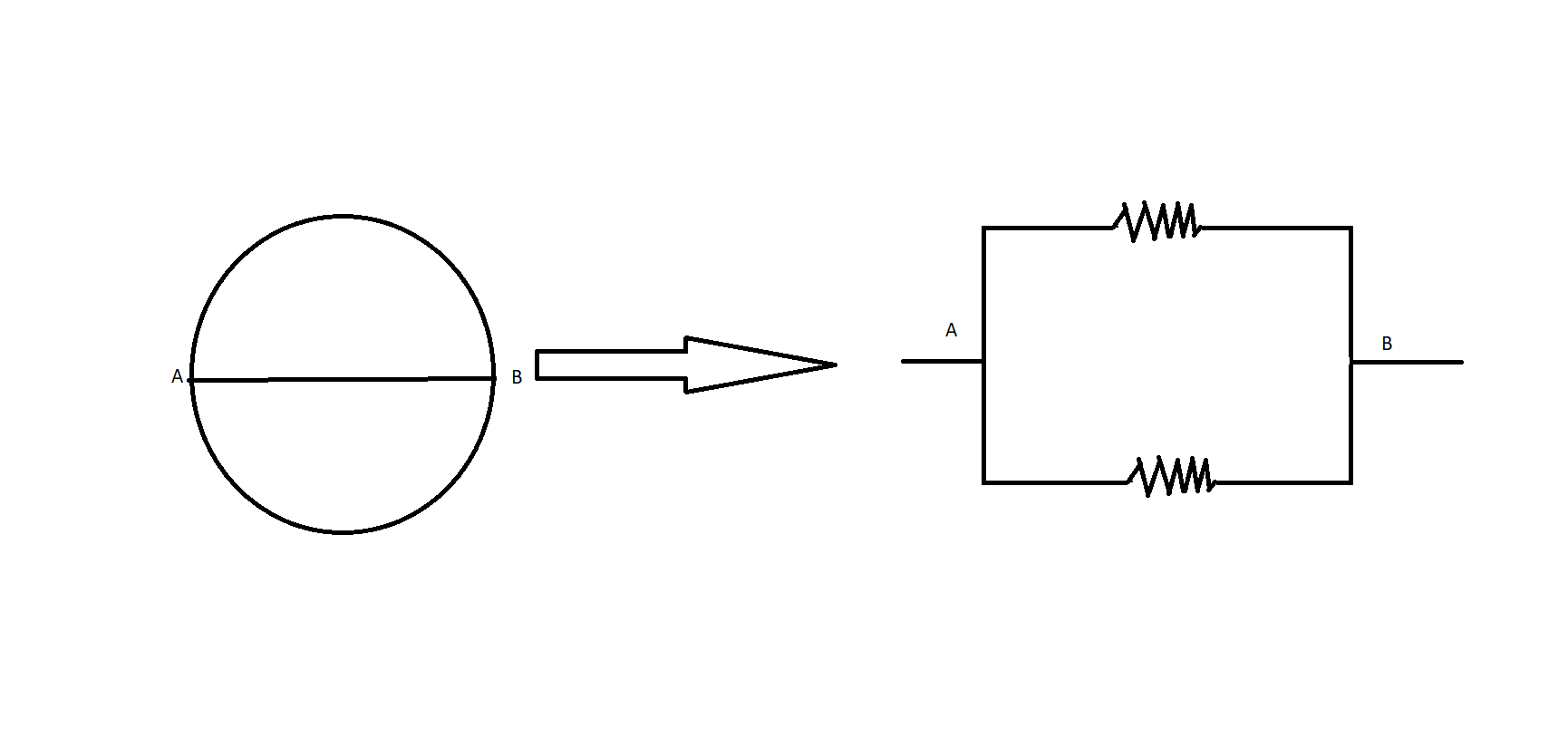
From the above figure, it can be concluded that the two arcs of the circle act as two parallel resistors across its diameter $AB$.
So the net resistance across the diameter will be,
$\Rightarrow \dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$
Where ${R_1}$ and ${R_2}$ are the resistance of the arcs connected in parallel, and $R$ is the net resistance of the wires across the diameter.
$\Rightarrow \dfrac{1}{R} = \dfrac{1}{4} + \dfrac{1}{4}$
$\Rightarrow R = 2\Omega$
So the resistance across the diameter will be $2\Omega$.

Note: The formulae, $\dfrac{{{R_1}}}{{{l_1}}} = \dfrac{{{R_2}}}{{{l_2}}}$, (Where ${R_1}$ and ${R_2}$ are the resistance of the wire and ${l_1}$ and ${l_2}$ are the length of the wire) is used only when the wires are made up of the same materials and have the same specification. This is because the resistivity of different wire, made up of different materials, will not be the same. Here, as the cross-section of the wire is uniform throughout the individual cross-section areas of the two semicircular wires will be equal and thus get canceled.