Question

A wire of resistance 5 ohm is bent in the form of a closed circle. What is the resistance between 2 points at the ends of any diameter of the circle?

Answer 1

Hint – Net resistance in parallel combination is $\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}}....$ potential across each resistor is same. And in series combination is $R = {R_1} + {R_2} + {R_3}...$ in series combination the current is flowing constant through each element.

Complete answer:
Formula used - $\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}}....$
Given, initial resistance= $5\Omega$

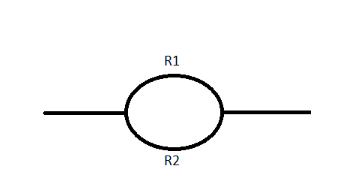
On dividing across diameter the length of the resistor halves and we know that $R$ is directly proportional to length of the element, hence the resistor on each side equals to $2.5\Omega$.Moreover, across the diameter they form parallel combinations.

$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} \\\ {R_1} = {R_2} = R \\\$

Since the same resistance is divided into two equal parts so those are equal.

So, the equation is,

$\dfrac{1}{{{R_{eq}}}} = \dfrac{2}{R} \\\ {\text{so,}} \\\ {R_{eq}} = \dfrac{R}{2} \\\$

$R = 2.5\Omega \\\ {R_{eq}} = \dfrac{{2.5}}{2}\Omega = 1.25\Omega \\\$

Hence, the answer to this question is$1.25\Omega$.

Note – In these types of questions each resistance of the same value and n such resistors are connected in parallel combination, the net resistance is equal to $\dfrac{1}{n}$ times the resistance of a single resistor.