Question

A wire of resistance $20\Omega$ is bent to form a closed square. What is the resistance across a diagonal of the square.

Answer 1

Resistance is defined as the property of a conductor to oppose current flow. It is denoted by R. So, in this question we will first find the resistance of all sides of the square and then we will solve the circuit in the manner so that we can get the resistance across the diagonal of the square.

Complete step-by-step answer:
We already know that the number of resistances present depends on how many sides are there in a square. So, we know that a square have 4 sides that-is-why, the wire resistance will be divided by 4.
${{R} ^ {'}} =\dfrac {20} {4} =5\Omega$
Here, R = resistance of a wire
$\therefore$ All sides of square will have a resistance of$5\Omega$.
Let, Resistance of all sides of square is R1 and resistance of diagonal of the square be R2 as shown in figure 1.

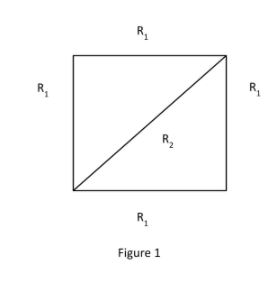
So, by solving figure i.e. by solving 2 resistances in series, we get –
${{R} _ {1}} ^ {'} =\, 5+5=10\Omega$ and,
${{R}_{2}}=\sqrt{{{5}^{2}}+{{5}^{2}}}=5\sqrt{2}$
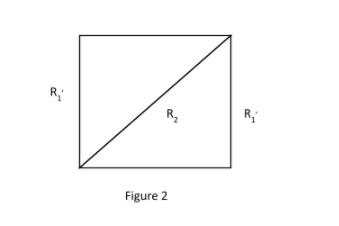
Now from figure 2, we get to see that the resistances R2 and R1’ are in parallel, so we can write:
$\begin{aligned} & \dfrac{1}{R}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}} \\\ & \Rightarrow \dfrac{1}{R}=\dfrac{1}{10}+\dfrac{1}{5\sqrt{2}} \\\ & \Rightarrow \dfrac {1} {R} =\dfrac {(\sqrt{2}+\sqrt{2})}{10\times \sqrt{2}} \\\ & \Rightarrow \dfrac{1}{R}=\dfrac{2}{10} \\\ & \Rightarrow \dfrac{1}{R}=\dfrac{1}{5} \\\ & \Rightarrow R=5\Omega \\\ \end{aligned}$
Hence, the resistance of the diagonal of a square will be $R=5\Omega$

Note: We should know the basics of resistance. The most important concept of resistance is its series and parallel operation, we must memorize its formula. In parallel connection of resistances, we add the reciprocal of two or more resistances and in series connection of resistances, we simply add two or more resistances together.