Question
Question: A wire of mass m and length l can slide freely on a pair of smooth, vertical rails. A magnetic field...
A wire of mass m and length l can slide freely on a pair of smooth, vertical rails. A magnetic field B exists in the region in the direction perpendicular to the plane of the rails. The rails are connected at the top end by the capacitor of capacitance C. Find the acceleration of the wire neglecting any electric resistance.
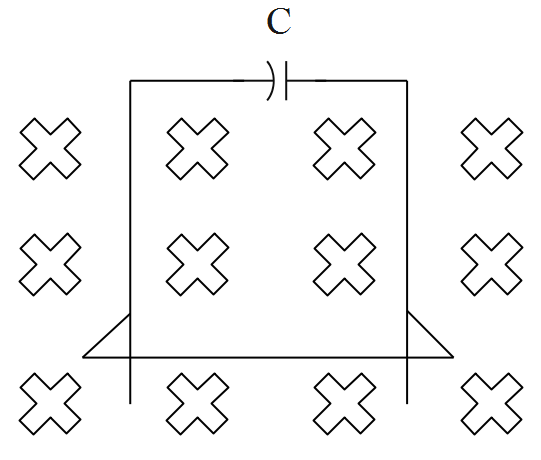
Solution
The emf induced in the rod gives the relation between the magnetic field, the length of the rod and the velocity of the electron. The potential difference across the terminals of the capacitor and the ends of the rod will be the same, as they are in parallel. The current in the circuit is the rate of change of charge. The force on the rod due to the magnetic field and its weight are in the opposite directions. Using these equations, we can find the acceleration.
Complete step-by-step solution:
The emf induced in the rod gives the relation between the magnetic field, the length of the rod and the velocity of the electron.
e=Blv
The potential difference across the terminals of the capacitor and the ends of the rod will be the same, as they are in parallel.
