Question

A wire of mass 100g length 1m and current 5A is balanced in mid air by a magnetic field B, then, find the value of B?
A. 0.2T
B. 0.1T
C. 0.5T
D. 0.6T

Answer 1

Firstly recall the expression for magnetic force and also the expression for force due gravity on a body. Since the wire is balanced in the air, we know that the magnetic force balances the force due to gravity. Now you could equate both expressions and then substitute the values to get the answer.
Formula used:
Expression for magnetic force,
${{F}_{B}}=I\left( l\times B \right)$

Complete answer:
In the question we are given a wire of mass 100g and length 1m. Also, there is a current I flowing through this wire. This wire is being balanced in the air by a magnetic field B and we are asked to find the value of this field. Let us represent the given system in a figure.

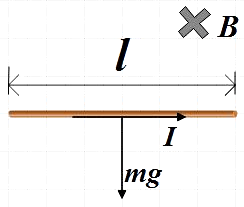
As we know that the current carrying wire is balanced in air, there should also be some force that is present so as to balance the wire against its weight. We know that anybody in the gravitational field has its weight acting downward. Since we are given that the magnetic field is responsible for balancing the wire in air, it should be the magnetic force due to this field that balances the weight acting downward.
We know that the magnetic force due to field B is given by,
${{F}_{B}}=I\left( l\times B \right)$……………………….. (1)
Where, $l$ is a vector of magnitude of the length of the wire and direction as that of current $I$.
But from the figure we see that the magnetic field perpendicular to the length of the wire, that is, the angle between them is $90{}^\circ$, so,
$l\times B=\left| l \right|\left| B \right|\sin \theta =\left| l \right|\left| B \right|\sin 90$
$l\times B=\left| l \right|\left| B \right|$
Where, $\left| l \right|$ and $\left| B \right|$ are magnitudes of length and magnetic field. Now, (1) becomes,
$\Rightarrow {{F}_{B}}=BIl$ ………………………….. (2)
We know that force due to gravity is given by,
${{F}_{g}}=mg$ …………………………… (3)
We have found that the upward magnetic force balances the force due to gravity, therefore,
$\Rightarrow {{F}_{B}}={{F}_{g}}$
$\Rightarrow BIl=mg$
$\Rightarrow B=\dfrac{mg}{Il}$
Substituting the given values from question,
$\Rightarrow B=\dfrac{100\times {{10}^{-3}}\times 10}{5\times 1}$
$\Rightarrow B=\dfrac{1}{5}=0.2T$
Therefore, the value of the given magnetic field is 0.2T.

So, the correct answer is “Option A”.

Note:
We know that a cross product of two vectors results in a vector that is mutually perpendicular to both of them. Also, the right hand rule gives you the direction of the magnetic force directly. If you point the index finger in the direction of current, middle finger in the direction of magnetic field then the thumb gives you the direction of magnetic force by right hand rule.