Question
Question: A wire of length \(l\) and mass \(m\) is bent in the form of a semicircle. The gravitational field i...
A wire of length l and mass m is bent in the form of a semicircle. The gravitational field intensity at the centre of semicircle is:
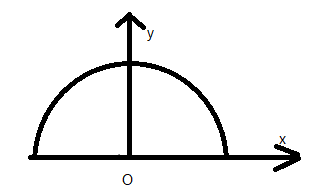
Solution
We know that the gravitational field is a vector which has two components. The perpendicular and the vertical component of the vector. Due to the symmetry of the semi-circle, we can say that one of the components gets cancelled.
Formula used:
E=0∫πdEsinθ
Complete step-by-step answer:
We know that the gravitational field is a non-contact force. We know that gravitational force is given as F=r2−GMm, where G is the gravitational constant, M and m is the mass of the bigger and the smaller objects which are at a distance r with respect to each other.
Then the electric field is given as, E=MF
Consider a bent wire of length land mass m, let us assume that the radius of the semicircle be R. Consider the gravitational field intensity at the centre of the semicircle O. Due to the symmetry of the semicircle clearly the x component of the cancels each other. Thus the total gravity field is along the y-axis only.
Let us assume that l=πR.
We know that the gravitational field, since the mass is distributed continuously on the ring, it is given as E=0∫πdEsinθ
