Question

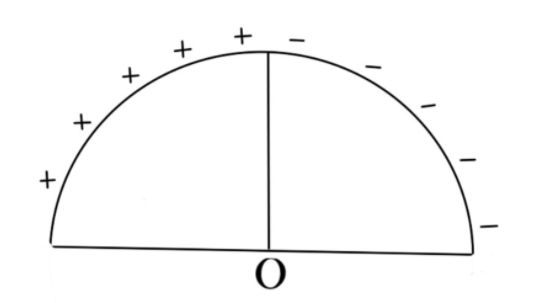
A wire of length $L = 20cm$, is bent into a semi-circular arc. If the two equal halves, of the arc, were each to be uniformly charged with charges $\pm Q$, $\left| Q \right| = {10^3}{\varepsilon _0}$ coulomb where ${\varepsilon _o}$ is the permittivity (in SI unit) of free space. Find the net electric field at the centre O of the semicircular ark.

a. $\left( {25 \times {{10}^3}N/C} \right)i$
b. $\left( {25 \times {{10}^3}N/C} \right)j$
c. $\left( {50 \times {{10}^3}N/C} \right)i$
d. $\left( {50 \times {{10}^3}N/C} \right)j$

Answer 1

Use the formula for the electric field by an arc of the loop. Here you have to find the linear charge density by dividing the total charge on the arc to the total length of the arc that is given as L.

Complete step by step answer:
First, we will calculate the electric field by a semicircle.
$E = \dfrac{{2k\lambda }}{r}\sin \dfrac{\theta }{2}$
Where,
$k = \dfrac{1}{{4\pi {\varepsilon _0}}}$
$\lambda =$linear charge density$= \dfrac{Q}{L} = \dfrac{{2 \times {{10}^3}{\varepsilon _0}}}{{0.2}}C/m$
$r =$radius of loop$= \dfrac{1}{{5\pi }}$
$L = \pi r \Rightarrow r = \dfrac{L}{\pi } = \dfrac{{0.2}}{\pi }$
$\theta =$arc angle$= \dfrac{\pi }{2}$

Electric field is given by
$E = \dfrac{{2\dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{2 \times {{10}^3}{\varepsilon _0}}}{{0.2}}}}{{\dfrac{1}{{5\pi }}}}\sin \dfrac{\pi }{2}$

$E = 25 \times {10^3}N/C$

We know that, electric field emerges from positive charge and terminates at negative charge. So electric field by positive arc at centre is away from arc and electric field by negative arc at the centre is towards the negative arc as shown in the figure below.

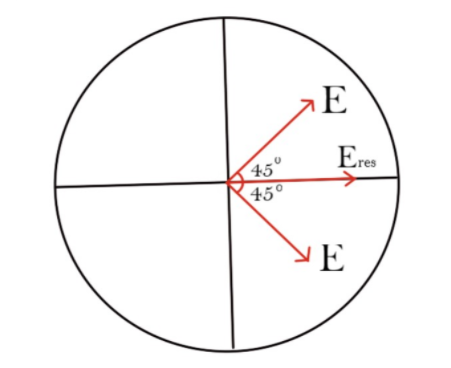
The direction of the resultant electric field is in the positive x direction as shown in the figure.
$E = \left( {25 \times {{10}^3}N/C} \right)i$, is correct

Note: Sometimes students replace the charged arcs with point charges with the same magnitude which is wrong concept because electric field also depends on the distribution of the charge in space.