Question

A wire of length $2{{L}_{{}}}$, is made by joining two wires of $A$ and $B$ of same length but different radii $r$ and $2r$ and made of the same material it is vibrating at a frequency such that the joint of the two wires forms a node. If the number of antinodes in wire $A$ is $p$ and that of $B$ is $q$ then ratio of $p:q$ is

$A.4:9$
$B.3:5$
$C.1:4$
$D.1:2$

Answer 1

We should apply the concept of densities for both the wires. The concept of linear density has to be used in solving this problem. Linear density of a material is defined as the mass per unit length. The relation of wavelength in terms of tension and linear density should be used to solve the problem.

Formula used:
We will use the following listed formulae to get to the correct answer:-
$\mu =\dfrac{\rho \times \pi {{r}^{2}}L}{L}$, $V=\sqrt{\dfrac{T}{\mu }}$ and $\nu =\dfrac{V}{2L}$.

Complete answer:
As both the wires are made up of the same material, so the density of both the wires are the same and denoted with $\rho$. Diagram is given below:-

For the first wire we have length equal to $L$ and radius equal to $r$. Now, we will calculate linear density, ${{\mu }_{A}}$ of the first wire with the following relation:-
${{\mu }_{A}}=\dfrac{\rho \times \pi {{r}^{2}}L}{L}$
Let ${{\mu }_{A}}=a$ ……………. $(i)$
Tension, $T$ in both the wires are also the same.
Now, we will calculate the speed of wave, ${{V}_{A}}$ of wire $A$ with the following relation:-
${{V}_{A}}=\sqrt{\dfrac{T}{{{\mu }_{A}}}}$
From $(i)$, we have
${{V}_{A}}=\sqrt{\dfrac{T}{a}}=V$ ………………….. $(ii)$
For the second wire we have length equal to $L$ and radius equal to $2r$. Now, we will calculate linear density, ${{\mu }_{B}}$ for the second wire using following relation:-
${{\mu }_{B}}=\dfrac{\rho \times \pi {{(2r)}^{2}}L}{L}$
${{\mu }_{B}}=\dfrac{\rho \times \pi 4{{r}^{2}}L}{L}$
Let ${{\mu }_{B}}=4a$…………. $(iii)$
Now calculating speed of wave, ${{V}_{B}}$ for the second wire with the following given relation:-
${{V}_{B}}=\sqrt{\dfrac{T}{{{\mu }_{B}}}}$
From $(ii)$, we have
${{V}_{B}}=\sqrt{\dfrac{T}{4a}}=\dfrac{V}{2}$…………. $(iv)$ (As we have taken $V=\sqrt{\dfrac{T}{a}}$ above)
Now, the fundamental frequency, ${{\nu }_{A}}$ in the wire $A$ is given as follows:-
${{\nu }_{A}}=\dfrac{{{V}_{A}}}{2L}$
From $(ii)$, we have
${{\nu }_{A}}=\dfrac{V}{2L}$…………….. $(v)$
Now, fundamental frequency, ${{\nu }_{B}}$ in the second wire is given as follows:-
${{\nu }_{B}}=\dfrac{{{V}_{B}}}{2L}$
From $(iv)$ we have
${{\nu }_{B}}=\dfrac{V}{4L}$……………..$(vi)$
LCM of both the frequencies comes out to be $\dfrac{V}{2L}$ which is the frequency at which both resonate.
Hence the number of loops in $A$ and B are in the ratio of $1:2$.

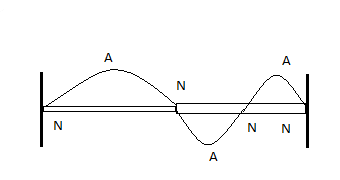
We can clearly see that node $(N)$ is a point where the wave has minimum amplitude and antinode $(A)$ is a point where the wave has maximum amplitude. We can clearly see that node $(N)$ is a point where the wave has minimum amplitude and antinode $(A)$ is a point where the wave has maximum amplitude.

So, the correct answer is “Option D”.

Note: Dimensions should be applied carefully. Never be confused between linear density and density (mass density) as they are different terms. Concept of resonant frequency should be applied. Resonance frequency is the oscillation of a system at its natural resonance. Resonance does occur when the system stores and transfers energy between different storage modes.