Question

A wire of length 1 meters and radius 1mm is subjected to a load. The extension is x. The wire is melted and then drawn into a wire of square cross-section of side 1mm. What is the extension under the same load?
A. ${\pi ^2}x$
B. $\pi {x^2}$
C. $\pi x$
D. $\dfrac{\pi }{x}$

Answer 1

In this question, we need to determine the extension in the wire when a load is subjected to the wire of square cross-section. For this, we will use the concept that the volume of the material will remain constant for both the shapes of the wire and then apply the young modulus formula $y = \dfrac{{F\ell }}{{A\vartriangle \ell }}$.

Complete step by step answer:
For the cyclical wire, the given date is as follows:
The length of the wire is say ${\ell _1} = 1m$
The radius of the wire is say $r = 1mm = 1 \times {10^{ - 3}}m$

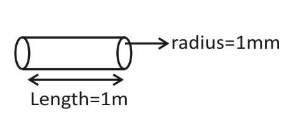
When this cylindrical cross-section area wire is subjected to a load, then the extension in the wire is given ‘x’.Now, this cylindrical cross section wire is melted and then drawn into a wire of square cross-section of side 1mm.

Now the same cylindrical wire is melted and reformed as a wire of square cross-section so the volume will remain unchanged.
$\therefore$The volume of circular cross section $=$volume of square cross-section
Mathematically, $\pi {r^2}{\ell _1} = \left( {{\ell _2}} \right) \times area{\text{ }}of{\text{ }}cross{\text{ }}section$
Substituting the values of the known values, i.e., ${l_1} = 1m = 1000mm,{\text{ }}r = 1mm{\text{ and A = 1}} \times 1$ in the equation $\pi {r^2}{\ell _1} = \left( {{\ell _2}} \right) \times area{\text{ }}of{\text{ }}cross{\text{ }}section$ to determine the length of the wire with the square cross-section area.
$\Rightarrow \pi {r^2}{\ell _1} = \left( {{\ell _2}} \right) \times area{\text{ }}of{\text{ }}cross{\text{ }}section \\\ \Rightarrow \pi {\left( 1 \right)^2} \times 1000 = \left( {{\ell _2}} \right) \times 1 \\\ \Rightarrow \left( {{\ell _2}} \right) = 1000\pi \\\$
Also, the material in initial and final condition (i.e., after melting and forming wire of square cross-section) is the same so,
Initial young modulus $=$final young modulus
Young modulus of cylindrical wire $=$young modulus of a cuboidal wire
${y_i} = {y_f}$if the load applied F, then
$\dfrac{{F{\ell _1}}}{{{A_1}x}} = \dfrac{{F{\ell _2}}}{{{A_2} \times \vartriangle {\ell _2}}}$
Where $\vartriangle {\ell _2}$is the extension into a cuboidal wire after applying load F,
So,
$\Rightarrow \dfrac{{{\ell _1}}}{{{A_1}x}} = \dfrac{{{\ell _2}}}{{{A_2} \times \vartriangle {\ell _2}}} \\\ \Rightarrow \dfrac{{{\ell _1}}}{{\left( {\pi {r^2} \times x} \right)}} = \dfrac{{1000\pi }}{{{A_2} \\\vartriangle {\ell _2}}} \\\ \Rightarrow \dfrac{{1000}}{{\pi {r^2}x}} = \dfrac{{1000\pi }}{{1 \times \vartriangle {\ell _2}}} \\\ \Rightarrow \dfrac{1}{{\pi \times 1 \times x}} = \dfrac{\pi }{{1 \times \vartriangle {\ell _2}}} \\\ \Rightarrow \vartriangle {\ell _2} = {\pi ^2}x \\\$
Hence, the extension in the wire having square cross section is given as ${\pi ^2}x$.
Hence,option A is the correct answer.

Note: When a wire is subjected to an external load, then it elongates. When the wire is melted and formed wire of different cross-sections, then volume remains the same because the density of the wire is the same before and after melting. When the material is the same, then the young modulus remains the same.