Question

A wire of cross-section A is stretched horizontally between two clamps located 2l meters apart. A weight W kg is suspended from the mid point of the wire. If the mid point sags vertically through a distance x << l the strain produced is

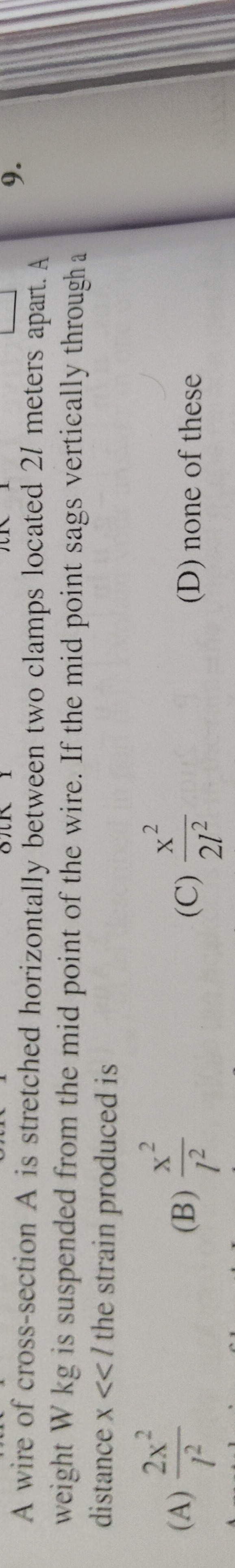
• A. $\frac{2x^2}{l^2}$
• B. $\frac{x^2}{l^2}$
• C. $\frac{x^2}{2l^2}$
• D. none of these

Answer 1

Answer: (C)

$\frac{x^2}{2l^2}$

Answer 2

The original length of the wire is $2l$. When the midpoint sags by a distance $x$, each half of the wire forms the hypotenuse of a right-angled triangle with base $l$ and height $x$. The length of one half of the stretched wire is $\sqrt{l^2 + x^2}$. The total length of the stretched wire is $2\sqrt{l^2 + x^2}$. The increase in length is $\Delta L = 2\sqrt{l^2 + x^2} - 2l$. Using the binomial approximation for $x << l$, $\sqrt{l^2 + x^2} \approx l(1 + \frac{x^2}{2l^2})$. Thus, $\Delta L \approx 2l(1 + \frac{x^2}{2l^2}) - 2l = \frac{x^2}{l}$. The strain is $\epsilon = \frac{\Delta L}{\text{Original Length}} = \frac{x^2/l}{2l} = \frac{x^2}{2l^2}$.