Question

A wire mesh consisting of very small squares is viewed at a distance of 8 cm through a magnifying converging lens of focal length 10 cm, kept close to the eye. The magnification produced by the lens is:
A. 5
B. 8
C. 10
D. 20

Answer 1

In this question distance of an object from a lens is given, and also its focal length is given, so we need to find the distance of the image formed, after which the magnification of the lens will be calculated. Magnification of a lens is the ratio of the distance of the object from the axis of the lens to the image distance given by the formula $m = \dfrac{v}{u}$

Complete step by step answer:
The focal length of the converging lens $f = 10cm$
The distance of the object from the converging lens $u = - 8cm$

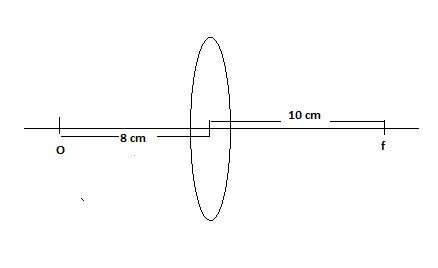
The focal length of a converging lens is given as
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u} - - (i)$
Here $v$is the distance of the image from the lens.
As we know the magnification of a lens is the ratio of the distance of the image formed from the axis of the lens to the distance of the object from the axis of the lens, given by the formula
$m = \dfrac{v}{u} - - (ii)$
Since the distance of the object is given, so we need to find the distance of the image formed from the axis by using equation (i)

$$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u} \\\ \dfrac{1}{v} = \dfrac{1}{f} + \dfrac{1}{u} \\\ = \dfrac{1}{{10}} + \dfrac{1}{{\left( { - 8} \right)}} \\\ = \dfrac{{8 - 10}}{{80}} \\\ = - \dfrac{2}{{80}} \\\ \dfrac{1}{v} = - \dfrac{1}{{40}} \\\$$

Hence the distance of the object from the lens $v = - 40cm$
Now find the magnification produced by the lens by using equation (ii)

$$m = \dfrac{v}{u} \\\ = \dfrac{{ - 40}}{{ - 8}} \\\ = 5 \\\$$

Hence magnification produced by the lens $m = 5$

Option A is correct.

Note: Students must note that if the image and objects are on the same side of the lens then the image distance is negative and the image formed is virtual, in the converging lens the focal length is positive.