Question

A wire KMN moves along the bisector of the angle $\theta$with a constant velocity v in a uniform magnetic field B perpendicular to the plane of the paper and directed inwards. Which of the following is correct?

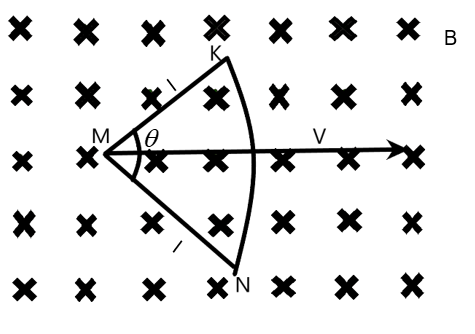
A) Effective length of the wire is $2l\sin \dfrac{\theta }{2}$
B) Emf induced between K and N is $2Blv\sin \dfrac{\theta }{2}$
C) The shape of KMN is immaterial, only the end points K and N are important.
D) All of the above.

Answer 1

We are given the direction of motion of a conducting wire in a magnetic field with its velocity in the field. We need to find the related changes that occur in this wire due to this motion in the given magnetic field such as the emf and the effective length.

Complete answer:
We know that any conductor moving in a magnetic field which has a perpendicular component of motion to the field can develop a motional emf along its two ends. A conductor moving with a constant velocity and in a constant angle will not produce a change in flux, so there will be no emf produced.
In our case a wire KMN is moving with a constant velocity with an angle, therefore, a motional emf is generated along its motion.
We know that the motional emf of a conductor is given as –
$\varepsilon =Blv$
Where, l is the effective length of the wire used.

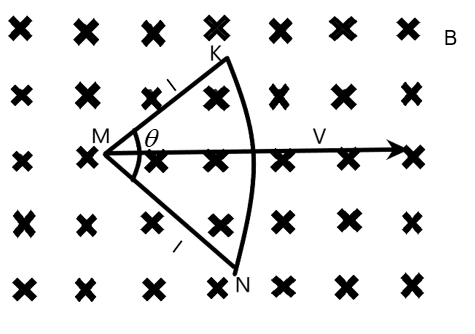
From the below figure, we can understand that the effective length of the wire is along $\sin \dfrac{\theta }{2}$, so the length will be $2l\sin \dfrac{\theta }{2}$, given that KM and MN is of length ‘l’.

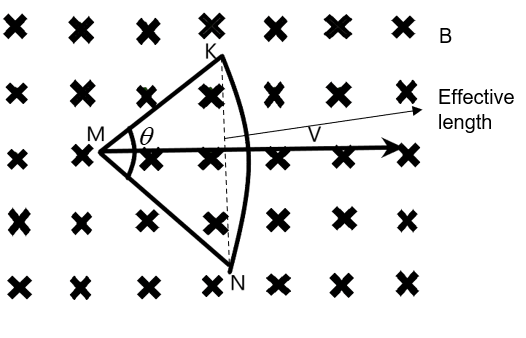
Now, let us calculate the motional emf of the wire KMN as –

& \varepsilon =l(v\times B) \\\ & \text{Here,} \\\ & l=2l \\\ & \Rightarrow \varepsilon =2Blv\sin \dfrac{\theta }{2} \\\ \end{aligned}$$ Also, we find from our observations that the KMN is immaterial, what matters is just the two end endpoints K and N. So, we have found that all the options in the question are true. **The correct answer is option D.** **Note:** We will find from the above exercise that the shape of the wire doesn’t account for the motional emf induced in it. It is the effective length which determines the amount of emf induced due to the movement of the conductor through the magnetic field.