Question
Question: A wire having mass m and length l can freely slide on a pair of parallel smooth horizontal rails pla...
A wire having mass m and length l can freely slide on a pair of parallel smooth horizontal rails placed in vertical magnetic field B. The rails are connected by a capacitor of capacitance C. The electric resistance of the rails and wires is zero. If constant force F acts on the wire as shown in the figure. Then acceleration of the wire can be given as-
(A) a=mC−2B2l−F
(B) a=CBl+mF
(C) a=mFC2B2l
(D) a=m+CB2l2F
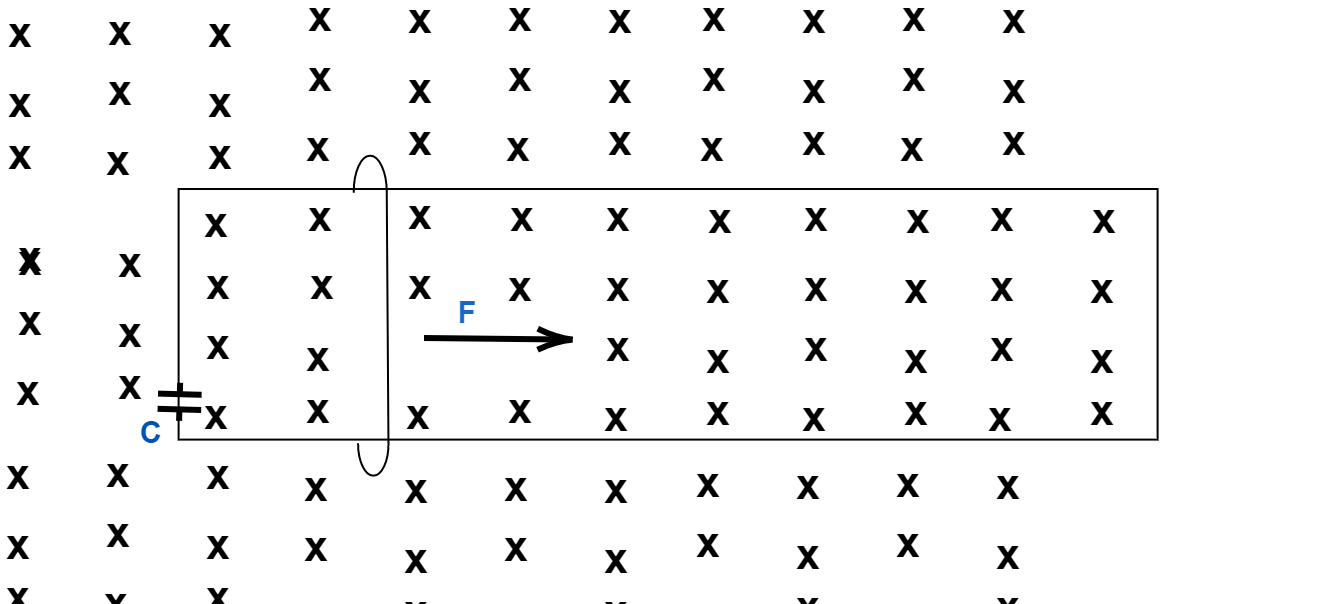
Solution
Hint When the wire is slid along the rails, an e.m.f. is developed in it. This difference in potential causes the capacitor to store a charge. The rate of change of this charge with respect to time gives the current flowing through the capacitor. This can be used to calculate the force on the wire and the net force is divided by m to give the value of acceleration.
Complete step by step answer:
The movement of the conductor perpendicular to a magnetic field produces an e.m.f. in it.
This e.m.f is given by-
ε=Bvl
Where B is the intensity of the Magnetic field.
v is the velocity of the wire
And l is the length of the wire.
This movement causes a flow of charge and this charge is stored in the capacitor.
Charge stored in a capacitor is given by-
Q=CV
Here V is the potential difference, which is equal to the produced e.m.f. ε.
Putting the value of εhere, we have-
Q=C(Bvl)
The rate of flow of charge is known as current, it can be obtained by differentiating the charge with respect to time.
Therefore,
i=dtdQ=BCl(dtdv)
The term dtdv is the acceleration of the wire, which can be represented by a therefore the current flow in the wire can be written as-
i=BCla
The same current also passes in the wire, so magnetic force (Fb) can be given by-
Fb=Bil
Fb=B(BCla)l
Fb=B2Cl2a
This makes the total forces acting on the wire two. On balancing the net force can be given by-
Fnet=F−Fb
ma=F−B2l2Ca
On rearranging,
F=a(m+B2l2C)
Therefore the acceleration is given by-
a=m+B2l2CF
Hence, option (D) is correct.
Note: The currents in both wires are assumed to be equal because there is a mention about no losses in the question, generally inductance has very less amount of losses but there is always a loss associated with a device.
