Question

A wire has $\alpha$ resistance per unit length and is arranged as shown. If side of the bigger square is l then equivalent resistance between points A and B will be

Answer 1

The length of bigger square is given to be ‘l’ units. The equivalent resistance will be the resistance from the sides of the bigger square as well as sides of smaller squares. Using trigonometry, find the length of the smaller square. Find the series and parallel combinations between different sides of the squares.

Complete step by step answer:
First of all, let us name the points where the smaller and bigger squares touch each other. The resultant diagram will be as follows:

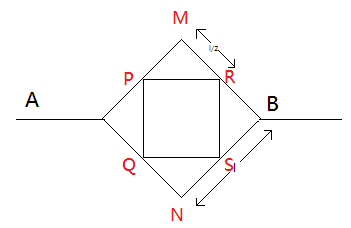
Here, P, Q, R and S are the points where the smaller and bigger squares touch each other. M and N are points taken for calculation purposes. Due to symmetry it is clear that the potential difference at point P and Q will be equal. Also, potential differences at point R and S will be equal. Mathematically this can be written as:
${V_p} = {V_Q}$ and ${V_R} = {V_S}$
Where ${V_P},\,{V_Q},\,{V_R},\,{V_S}$ are the potential differences across P, Q, R and S respectively.
The length of side $PM = RM = \dfrac{l}{2}$ this is given to us and $\angle PMR = {90^ \circ }$ , hence we can find length of side PR by using Pythagoras Theorem as follows:
$P{R^2} = P{M^2} + R{M^2}$
$\Rightarrow PR = \sqrt {P{M^2} + R{M^2}}$
$\Rightarrow PR = \sqrt {{{\left( {\dfrac{l}{2}} \right)}^2} + {{\left( {\dfrac{l}{2}} \right)}^2}}$
$\Rightarrow PR = \dfrac{l}{{\sqrt 2 }}$
Similarly, $PR = PQ = QS = RS$ as the inner figure is a square.
The resistances of the wires are given to be $\alpha$ per unit length.
Therefore, resistances across the lengths $AM = MB = BN = NA = \dfrac{{\alpha l}}{2}$
And the resistances across the lengths $PQ = QS = SR = PR = \dfrac{{\alpha l}}{{\sqrt 2 }}$
Now let us redraw the figure mentioning the resistances:

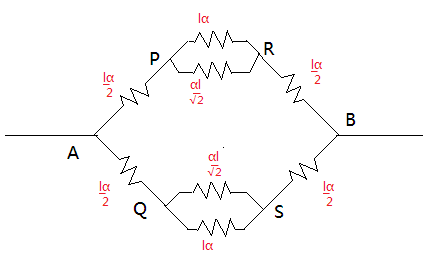
It is clear from the diagram that the resistances between PR are in parallel and resistances between QS are also in parallel. Hence, we will find the effective resistance using the formula for parallel combination as follows:
$\dfrac{1}{{{R_p}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$
Where ${R_p}$ is the effective resistance for ${R_1}$ and ${R_2}$ resistances being in parallel.
Applying the same formula for PR and QS, we get:
$\dfrac{1}{{{R_{PR}}}} = \dfrac{1}{{l\alpha }} + \dfrac{1}{{\dfrac{{l\alpha }}{{\sqrt 2 }}}}$
Where ${R_{PR}}$ is the effective resistance between point P and R
$\Rightarrow {R_{PR}} = \dfrac{{l\alpha }}{{\sqrt 2 + 1}}$
As there is symmetry and the resistances between PR and QS are equal, therefore we can have:
$\dfrac{1}{{{R_{QS}}}} = \dfrac{1}{{l\alpha }} + \dfrac{1}{{\dfrac{{l\alpha }}{{\sqrt 2 }}}}$
Where ${R_{QS}}$ is the effective resistance between point Q and S:
$\Rightarrow {R_{QS}} = \dfrac{{l\alpha }}{{\sqrt 2 + 1}}$
Observe the figure, we have resistances AP, PR and RB in series
And resistances AQ, QS and SB in series, while they both are parallel to each other:
Please follow the figure below:

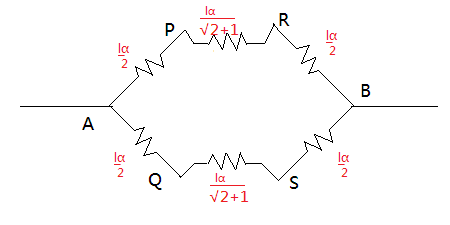
Lets first find the effective resistance between AB, since they are in series hence their resultant will be given as:
${R_{APRB}} = {R_{AP}} + {R_{PR}} + {R_{RB}}$
Where ${R_{APRB}},\,\,{R_{AP}},\,\,{R_{PR}},\,\,{R_{RB}}$ are the resistances between the mentioned subscripts
${R_{APRB}} = \dfrac{{l\alpha }}{2} + \dfrac{{l\alpha }}{{\sqrt 2 + 1}} + \dfrac{{l\alpha }}{2}$
$\Rightarrow {R_{APRB}} = \sqrt 2 l\alpha$
Similarly, the resultant resistance for AQ, QS. SB will be
${R_{AQSB}} = \sqrt 2 l\alpha$
Now ${R_{APRB}},\,{R_{AQSB}}$ are in parallel, hence their resultant will be calculated using parallel combination formula as follows:
$\dfrac{1}{{{R_{AB}}}} = \dfrac{1}{{{R_{APRB}}}} + \dfrac{1}{{{R_{AQSB}}}}$
$\Rightarrow \dfrac{1}{{{R_{AB}}}} = \dfrac{1}{{\sqrt 2 l\alpha }} + \dfrac{1}{{\sqrt 2 l\alpha }}$
$\therefore {R_{AB}} = \dfrac{{l\alpha }}{{\sqrt 2 }}$
This is the resultant resistance between point A and B.

Note:
For such types of circuits, always try to simplify the circuit by mentioning points wherever two wires are joining. For this question, the lengths are different. Each side of the square has some resistance. This system consists of two squares and the effective resistance is sum all the resistances of the sides.