Question
Question: A wire carrying current \[I\] is ted between two points P and Q and is in the shape of a circular ar...
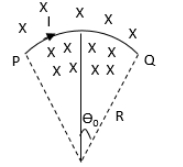
A wire carrying current I is ted between two points P and Q and is in the shape of a circular arc of radius R due to a uniform magnetic field B (perpendicular to the plane of paper, shown by xxx) in the vicinity of the wire. If the wire subtends an angle 2θ0 at the centre of the circle (of which it forms an arch) then the tension in the wire is:
A. IBR
B. sinθ0IBR
C. 2sinθ0IBR
D. sinθ0IBRθ0
Solution
Use the formula for the magnetic force acting on the current carrying wire. This formula gives the relation between the magnetic field, length of the wire and current. Consider the small element of length of the wire and determine the magnetic force on this length. Apply Newton’s second law of motion in the vertical direction to the wire and determine the value of tension in the wire.
Formula used:
The magnetic force F acting on a wire is
F=BIL …… (1)
Here, B is a magnetic field, I is current flowing in the wire and L is the length of the wire.
Complete step by step answer:
We have given that the current I flows through a current carrying wire which is tied between the points P and Q in the shape of a circular arc of radius R and the angle subtended by the arc of wire at the centre of the circle is 2θ0.Let L be the length of the wire.Let us consider a small element dL on the length of the current carrying wire and let this small element subtends a small angle dθ0 at the centre of the circle.Let us determine the magnetic force on this small element on the length of the wire.Substitute dL for L in equation (1).
F=BIdL
The direction of this magnetic force is acting radially outward from the centre of the arc.We can use the relation between the radius, length of arc and angle subtended at the centre.
2θ0=RdL
Let us draw a free body diagram of the wire.
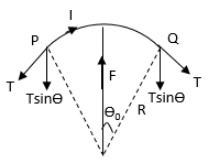
In the above free body diagram, T is the tension in the wire.Apply Newton’s second law of motion to the wire in vertical direction.
F=2Tsindθ0
Since the angle is very small, we can write
sindθ0=dθ0
Thus,
⇒F=2Tdθ0
Substitute BIdL for F in the above equation.
BIdL=2Tθ0
⇒BIdL=2T(22θ0)
⇒BIdL=T(2θ0)
Substitute RdL for 2θ0 in the above equation.
⇒BIdL=T(RdL)
∴T=IBR
Therefore, the tension in the wire is IBR.
Hence, the correct option is A.
Note: The students should keep in mind that the relation between angle, radius and arc length for the half of the angle subtended by the arc at the centre of the circle is the same for the whole angle subtended by the arc as the length of the wire and radius of the arc remains the same. Hence, we have replaced the whole angle subtended by the wire by the relation between the length of the small element and radius of the arc.
