Question

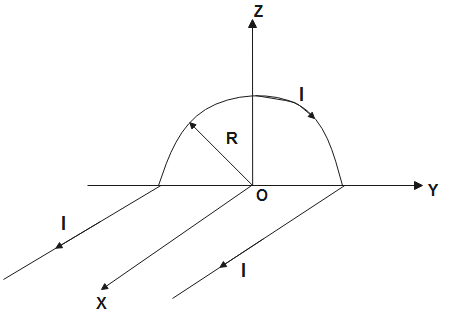
A wire carrying current $I$ has the shape as shown in the adjoining figure. Linear parts of the wire are very long and parallel to the x-axis while the semicircular portion of radius $R$ is lying in the Y-Z axis. Magnetic field at point O is-
(A). $\vec{B}=-\dfrac{{{\mu }_{0}}I}{4\pi R}(\mu \hat{i}\times 2\hat{k})$
(B). $\vec{B}=-\dfrac{{{\mu }_{0}}I}{4\pi R}(\pi \hat{i}+2\hat{k})$
(C). $\vec{B}=\dfrac{{{\mu }_{0}}I}{4\pi R}(\pi \hat{i}-2\hat{k})$
(D). $\vec{B}=\dfrac{{{\mu }_{0}}I}{4\pi R}(\pi \hat{i}+2\hat{k})$

Answer 1

Magnetic field at point O in space is the resultant of different magnetic fields due to current carrying elements. The magnetic field due to a current carrying element depends on the length, current, distance between the point and element and the angle between the line joining the element and point and the element.

Formula Used:
$B=\dfrac{{{\mu }_{0}}I}{4R}$
$B=\dfrac{{{\mu }_{0}}I}{4\pi R}$

Complete step-by-step solution:
The magnetic field due to different current carrying elements is different which can be derived using Biot Savart’s law of ampere circuit law.
According to the Biot Savart’s law,

When a conductor has current flowing through it, the magnetic field around it is-
$B\propto \dfrac{Idl\sin \theta }{{{r}^{2}}}$
Here,
$I$ is the current flowing through the conductor
$dl$ is the length of the current carrying element
$\theta$ is the angle between the line joining the point and element and the element
$r$ is the distance between the point and element

In space, there are three elements carrying current. The resultant magnetic field vector acting on point O is the sum of all the magnetic field vectors due to different elements in space.

The magnetic field due to a semicircular wire is given by-
$B=\dfrac{{{\mu }_{0}}I}{4R}$
Here, $B$ is the magnetic field
$I$ is the current flowing through the wire
$R$ is the radius of the wire
The right hand thumb rule tells us the direction of the magnetic field
The magnetic field due to due to a long straight current carrying wire at one end is given by-
$B=\dfrac{{{\mu }_{0}}I}{4\pi R}$
Here, $R$ is the distance of the point from the element

The magnetic field at point O due to the different elements is-
$\begin{aligned} & \vec{B}={{{\vec{B}}}_{1}}+{{{\vec{B}}}_{2}}+{{{\vec{B}}}_{3}} \\\ & \Rightarrow \vec{B}=\dfrac{{{\mu }_{0}}I}{4R}(-\hat{i})+\dfrac{{{\mu }_{0}}I}{4\pi R}(\hat{k})+\dfrac{{{\mu }_{0}}I}{4\pi R}(\hat{k}) \\\ & \Rightarrow \vec{B}=\dfrac{{{\mu }_{0}}I}{4\pi R}(-\pi \hat{i}+2\hat{k}) \\\ & \therefore \vec{B}=\dfrac{{{\mu }_{0}}I}{4\pi R}(\pi \hat{i}-2\hat{k}) \\\ \end{aligned}$

The resultant magnetic field vector acting on point O is $\dfrac{{{\mu }_{0}}I}{4\pi R}(\pi \hat{i}-2\hat{k})$.

Therefore, the correct option is (C).

Note:
Magnetic field at the axis of a long current carrying wire is zero. According to the right hand thumb rule; for a semicircular wire, if current is denoted by the fingers, direction of field is given by the thumb. For a straight wire, if the thumb is in the direction of current, then fingers represent the direction of the field.